pyvista.CellType

pyvista.CellType#

enum CellType(value)[source]#

Define types of cells.

Cells are defined by specifying a type in combination with an ordered list of points. The ordered list, often referred to as the connectivity list, combined with the type specification, implicitly defines the topology of the cell. The x-y-z point coordinates define the cell geometry.

Although point coordinates are defined in three dimensions, the cell topology can be 0, 1, 2, or 3-dimensional.

Cells can be primary (e.g. triangle) or composite (e.g. triangle strip). Composite cells consist of one or more primary cells, while primary cells cannot be decomposed.

Cells can also be characterized as linear or non-linear. Linear cells use linear or constant interpolation. Non-linear cells may use quadratic, cubic, or some other interpolation.

This enumeration defines all cell types used in VTK and supported by PyVista. The type(s) of cell(s) to use is typically chosen based on application need, such as graphics rendering or numerical simulation.

See also

VTK Book: Cell Types: VTK reference about cell types.
vtkCellType.h: List of all cell types defined in VTK.
Linear Cells: Detailed example using linear cells.
Unstructured Grid with Polyhedra: Example creating a mesh with POLYHEDRON cells.
Triangle Strips: Example creating a mesh with TRIANGLE_STRIP cells.
pyvista.examples.cells: Examples creating a mesh comprising a single cell.

Examples

Create a single cube. Notice how the cell type is defined using the CellType.

>>> import numpy as np
>>> from pyvista import CellType
>>> import pyvista as pv
>>> cells = np.array([8, 0, 1, 2, 3, 4, 5, 6, 7])
>>> cell_type = np.array([CellType.HEXAHEDRON], np.int8)
>>> points = np.array(
...     [
...         [0, 0, 0],
...         [1, 0, 0],
...         [1, 1, 0],
...         [0, 1, 0],
...         [0, 0, 1],
...         [1, 0, 1],
...         [1, 1, 1],
...         [0, 1, 1],
...     ],
...     dtype=np.float32,
... )
>>> grid = pv.UnstructuredGrid(cells, cell_type, points)
>>> grid
UnstructuredGrid (...)
  N Cells:    1
  N Points:   8
  X Bounds:   0.000e+00, 1.000e+00
  Y Bounds:   0.000e+00, 1.000e+00
  Z Bounds:   0.000e+00, 1.000e+00
  N Arrays:   0

Member Type:: int

Valid values are as follows:

EMPTY_CELL = <CellType.EMPTY_CELL: 0>#: Linear Primary 0D Points: 0 Edges: 0 Faces: 0

Used as a place-holder during processing.

See also vtkEmptyCell.

VERTEX = <CellType.VERTEX: 1>#: pyvista.examples.cells.Vertex

Linear Primary 0D Points: 1 Edges: 0 Faces: 0

Represents a point in 3D space.

The vertex is a primary zero-dimensional cell. It is defined by a single point.

See also vtkVertex.

POLY_VERTEX = <CellType.POLY_VERTEX: 2>#: pyvista.examples.cells.PolyVertex

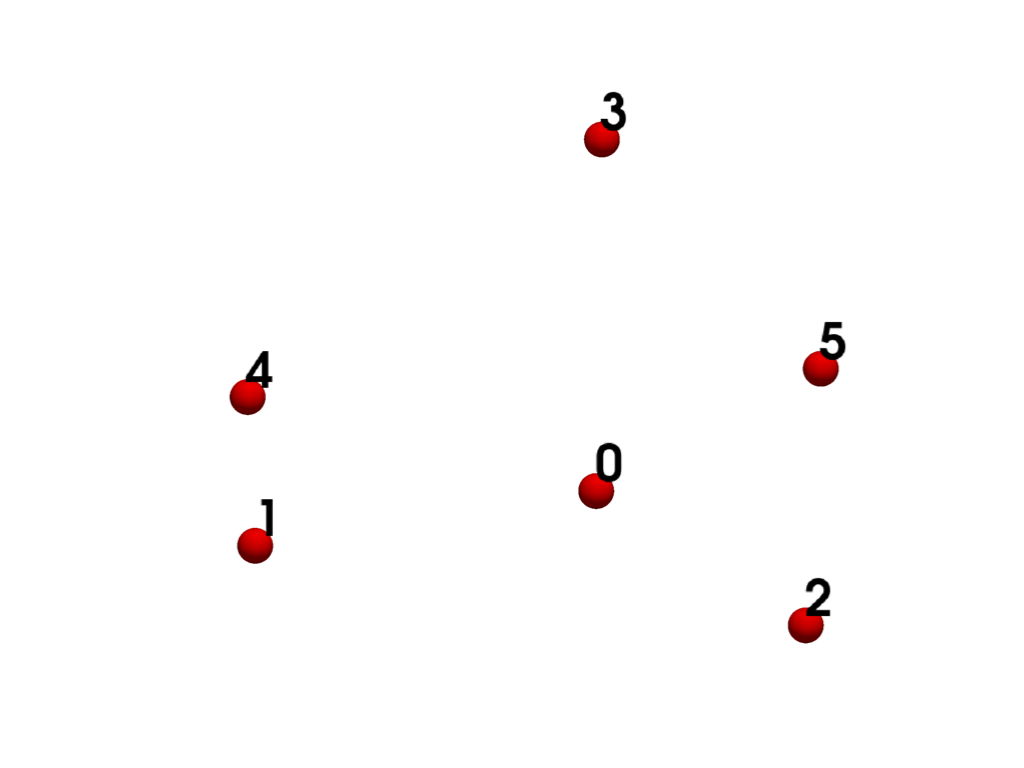
Linear Composite 0D Points: variable Edges: 0 Faces: 0

Represents a set of points in 3D space.

The polyvertex is a composite zero-dimensional cell. It is defined by an arbitrarily ordered list of points.

See also vtkPolyVertex.

LINE = <CellType.LINE: 3>#: pyvista.examples.cells.Line

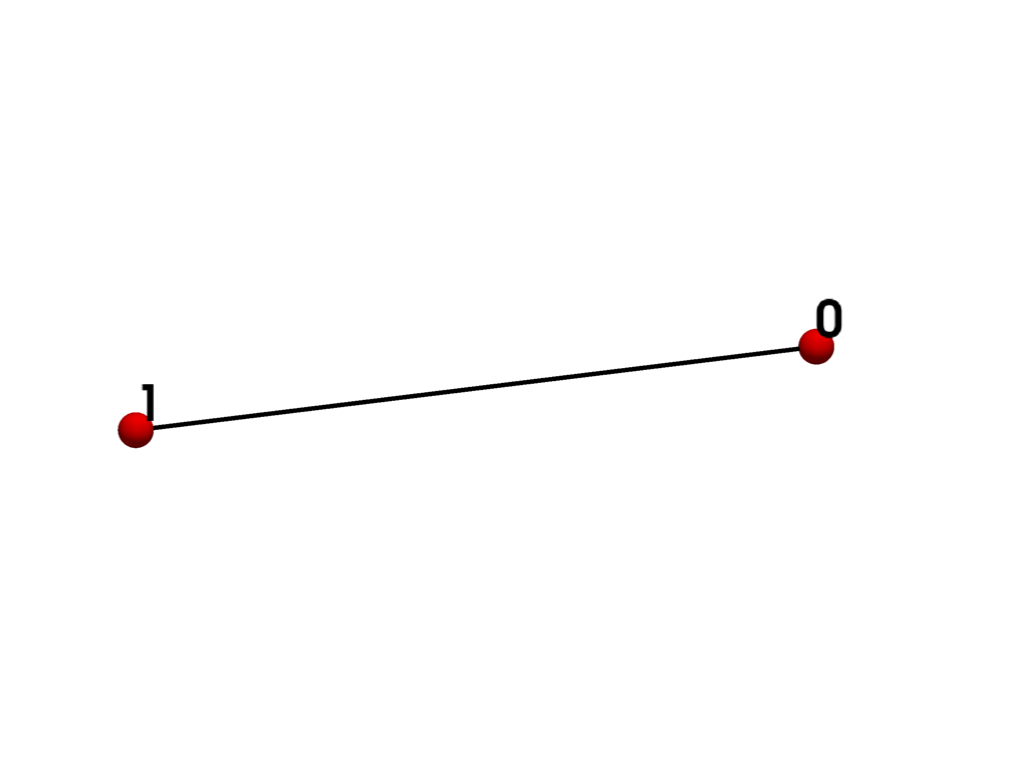
Linear Primary 1D Points: 2 Edges: 0 Faces: 0

Represents a 1D line.

The line is a primary one-dimensional cell. It is defined by two points. The direction along the line is from the first point to the second point.

See also vtkLine.

POLY_LINE = <CellType.POLY_LINE: 4>#: pyvista.examples.cells.PolyLine

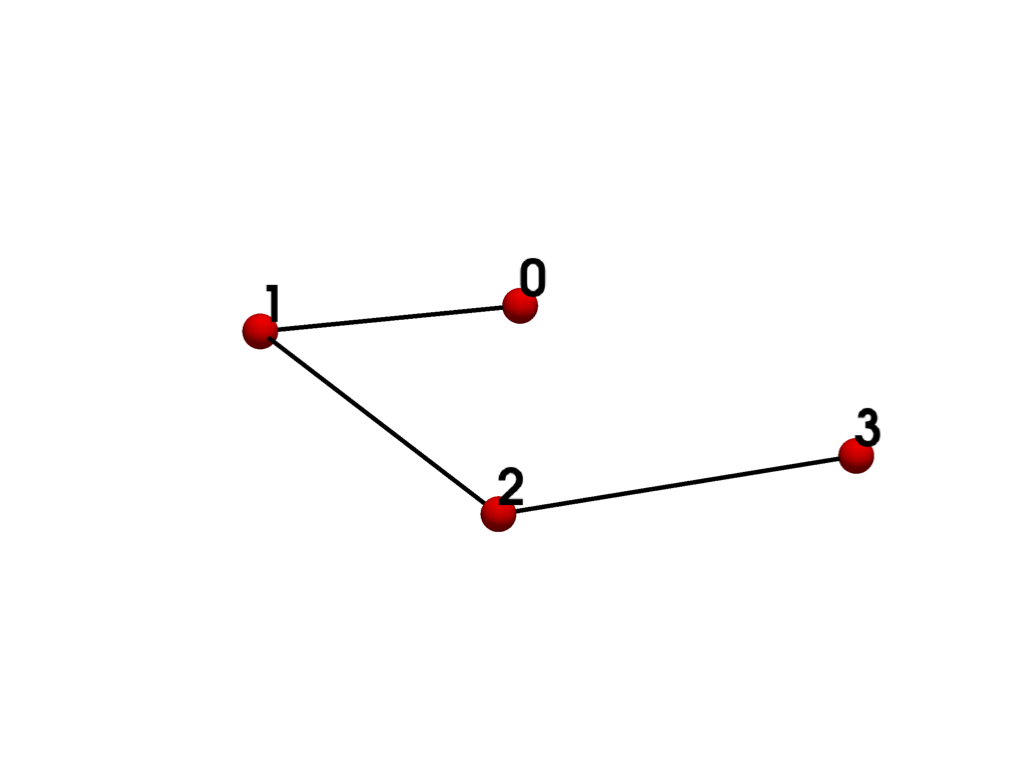
Linear Composite 1D Points: variable Edges: 0 Faces: 0

Represents a set of 1D lines.

The polyline is a composite one-dimensional cell consisting of one or more connected lines.

See also vtkPolyLine.

TRIANGLE = <CellType.TRIANGLE: 5>#: pyvista.examples.cells.Triangle

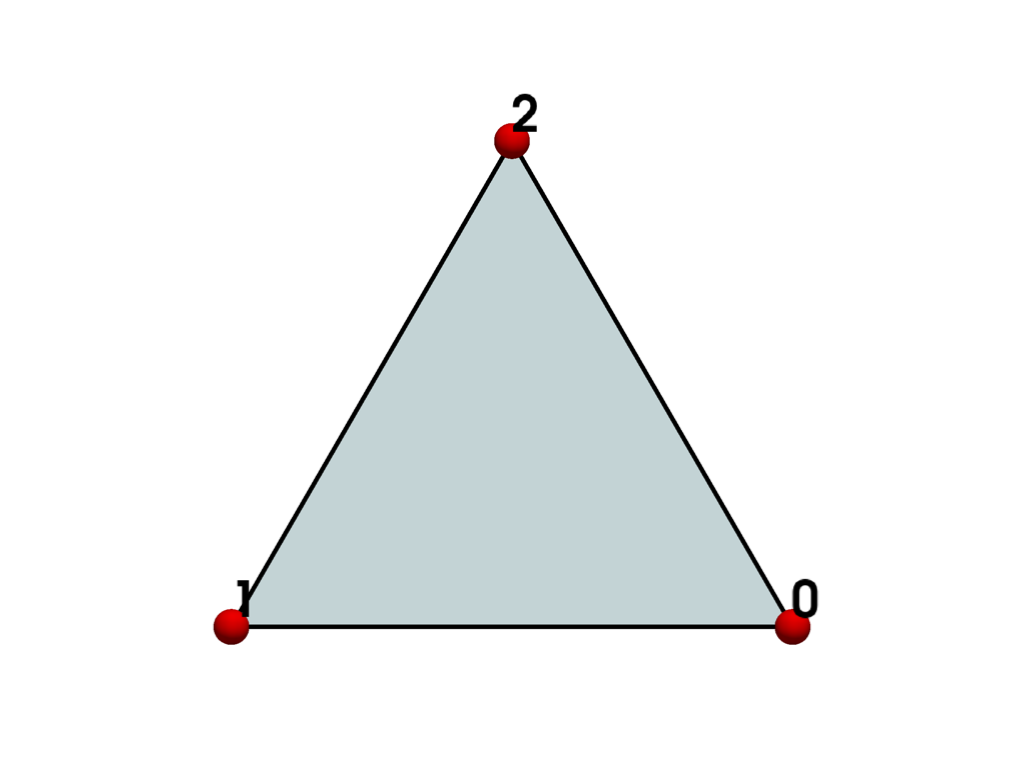
Linear Primary 2D Points: 3 Edges: 3 Faces: 0

Represents a 2D triangle.

The triangle is a primary two-dimensional cell. The triangle is defined by a counter-clockwise ordered list of three points.

See also vtkTriangle.

TRIANGLE_STRIP = <CellType.TRIANGLE_STRIP: 6>#: pyvista.examples.cells.TriangleStrip

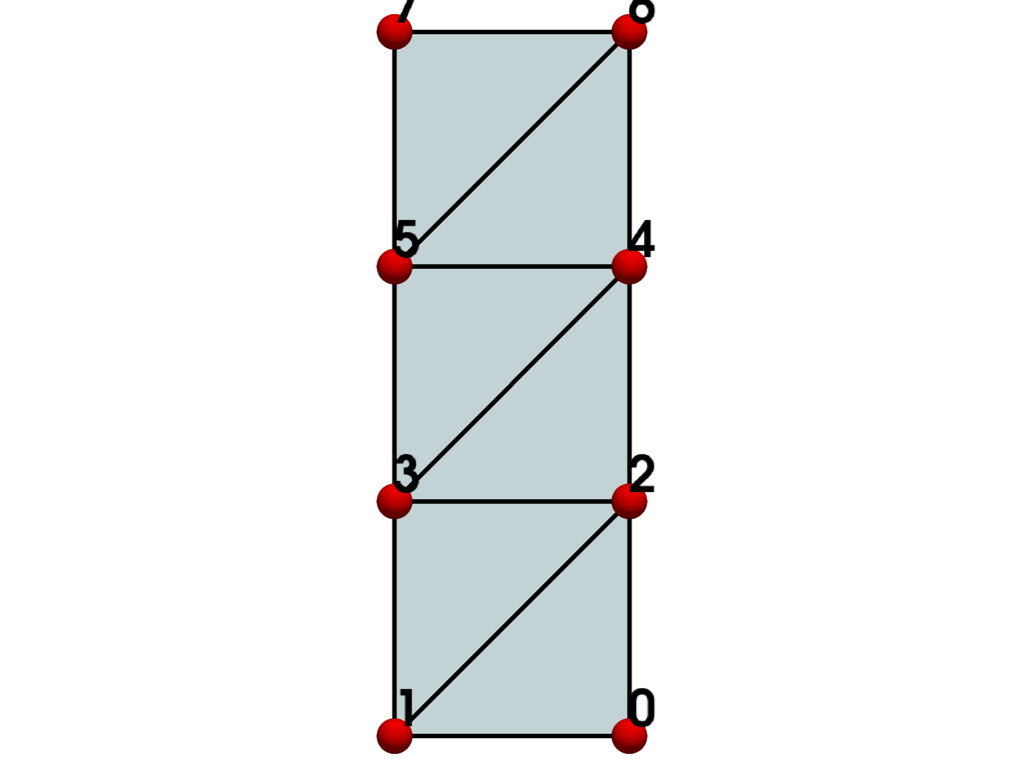
Linear Composite 2D Points: variable Edges: variable Faces: 0

Represents a 2D triangle strip.

The triangle strip is a composite two-dimensional cell consisting of one or more triangles. It is a compact representation of triangles connected edge-to-edge.

See also vtkTriangleStrip.

POLYGON = <CellType.POLYGON: 7>#: pyvista.examples.cells.Polygon

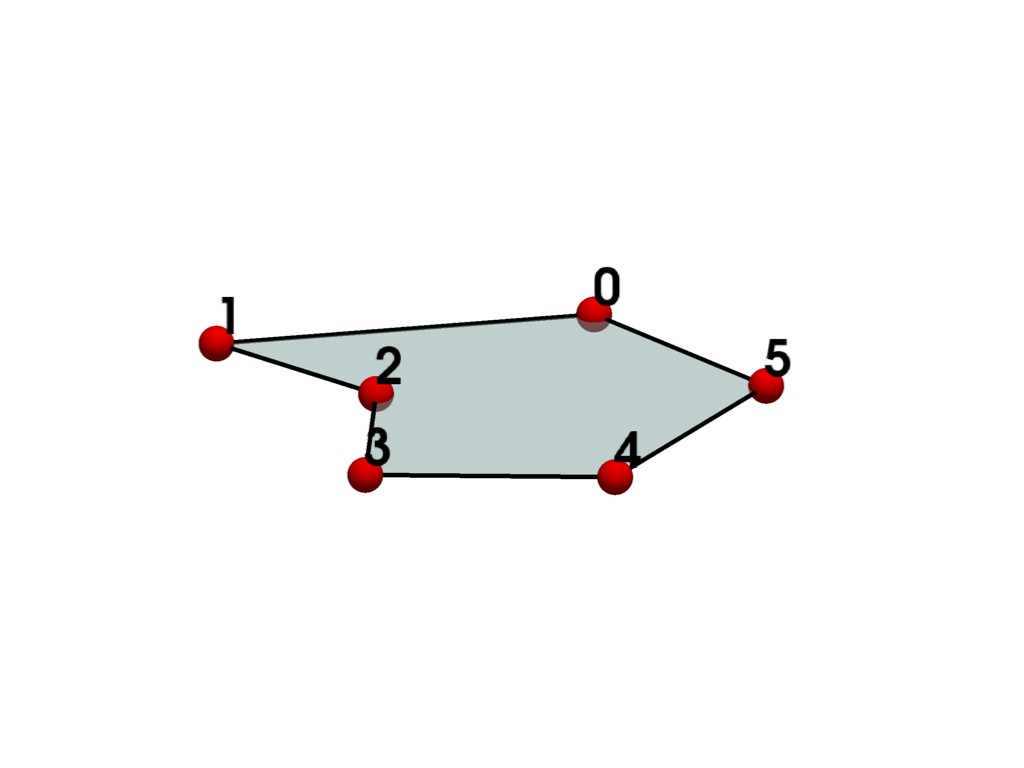
Linear Composite 2D Points: variable Edges: variable Faces: 0

Represents a 2D n-sided polygon.

The polygon is a primary two-dimensional cell. It is defined by an ordered list of three or more points lying in a plane.

See also vtkPolygon.

PIXEL = <CellType.PIXEL: 8>#: pyvista.examples.cells.Pixel

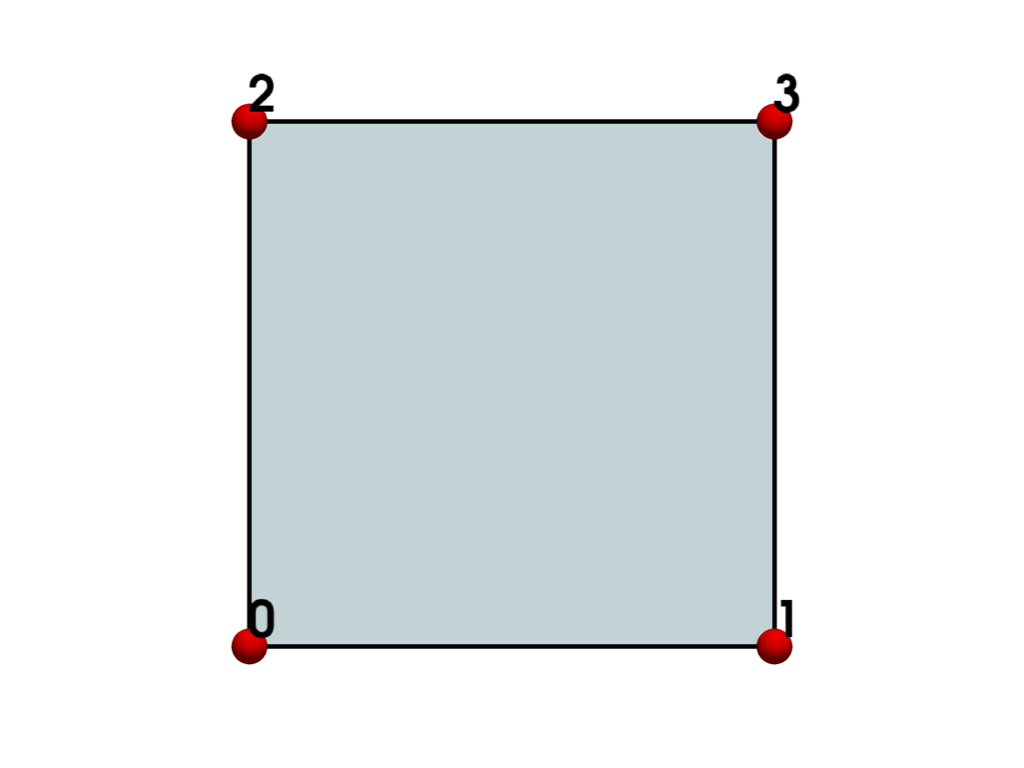
Linear Primary 2D Points: 4 Edges: 4 Faces: 0

Represents a 2D orthogonal quadrilateral.

The pixel is a primary two-dimensional cell defined by an ordered list of four points.

Warning

This definition of a pixel differs from the conventional definition which describes a single constant-valued element in an image. The meaning of this term can vary depending on context. See Image Data Representations for examples.

See also vtkPixel.

QUAD = <CellType.QUAD: 9>#: pyvista.examples.cells.Quadrilateral

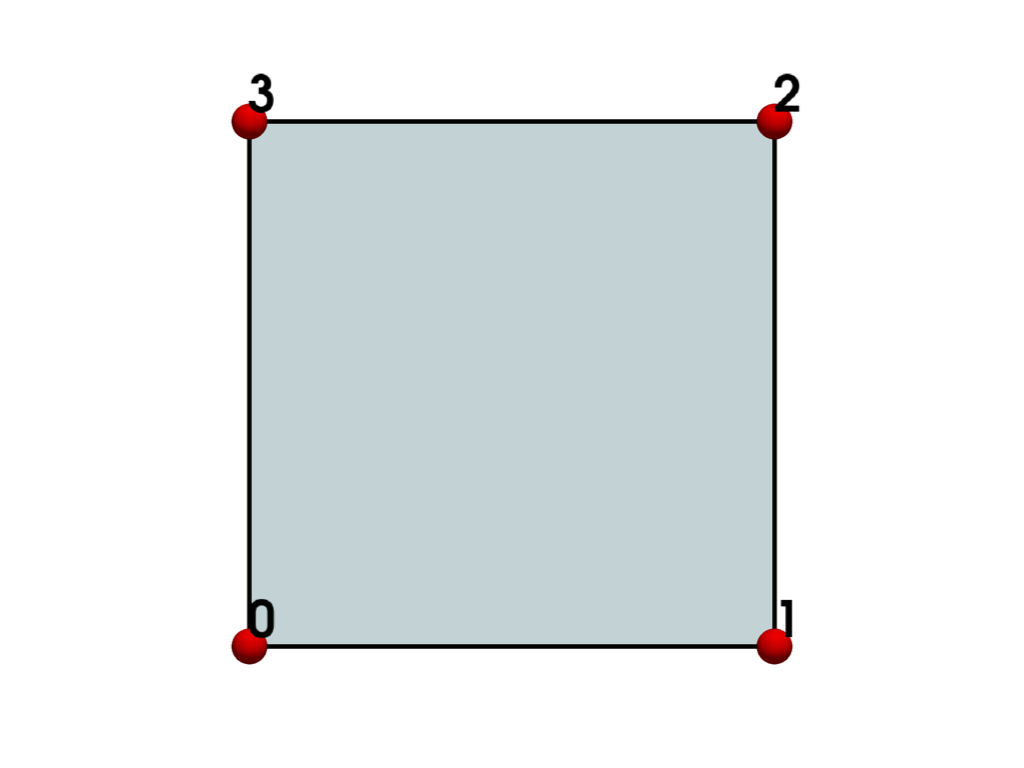
Linear Primary 2D Points: 4 Edges: 4 Faces: 0

Represents a 2D quadrilateral.

The quadrilateral is a primary two-dimensional cell. It is defined by an ordered list of four points lying in a plane.

See also vtkQuad.

TETRA = <CellType.TETRA: 10>#: pyvista.examples.cells.Tetrahedron

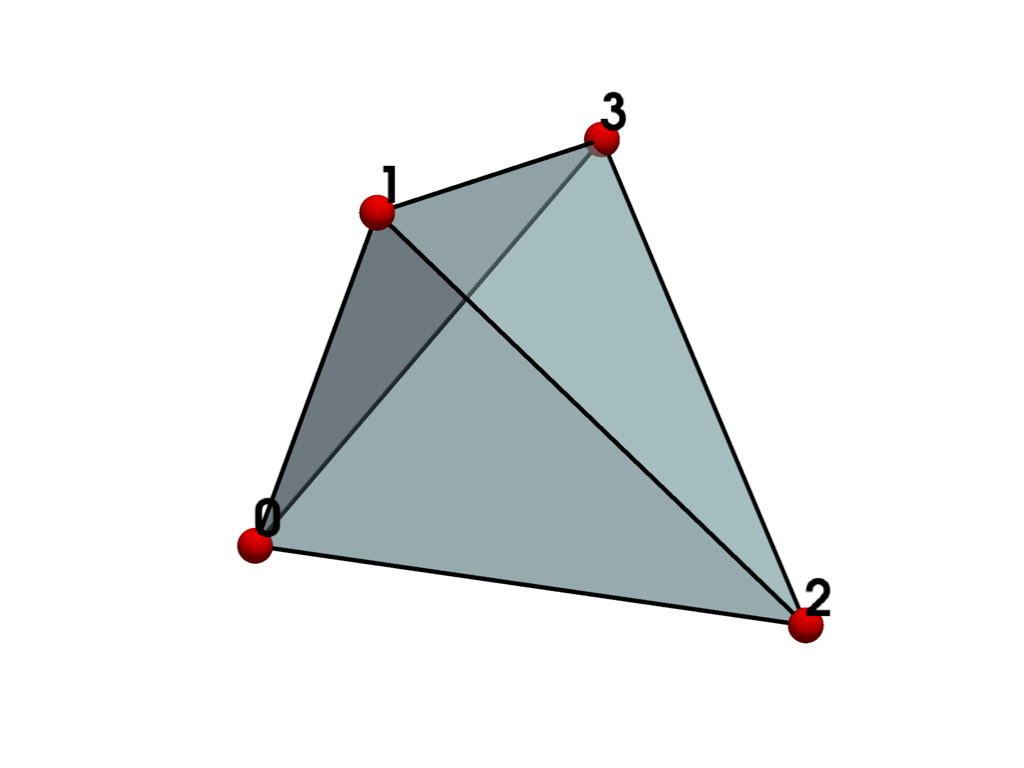
Linear Primary 3D Points: 4 Edges: 6 Faces: 4

Represents a 3D tetrahedron.

The tetrahedron is a primary three-dimensional cell. The tetrahedron is defined by a list of four non-planar points. It has six edges and four triangular faces.

See also vtkTetra.

VOXEL = <CellType.VOXEL: 11>#: pyvista.examples.cells.Voxel

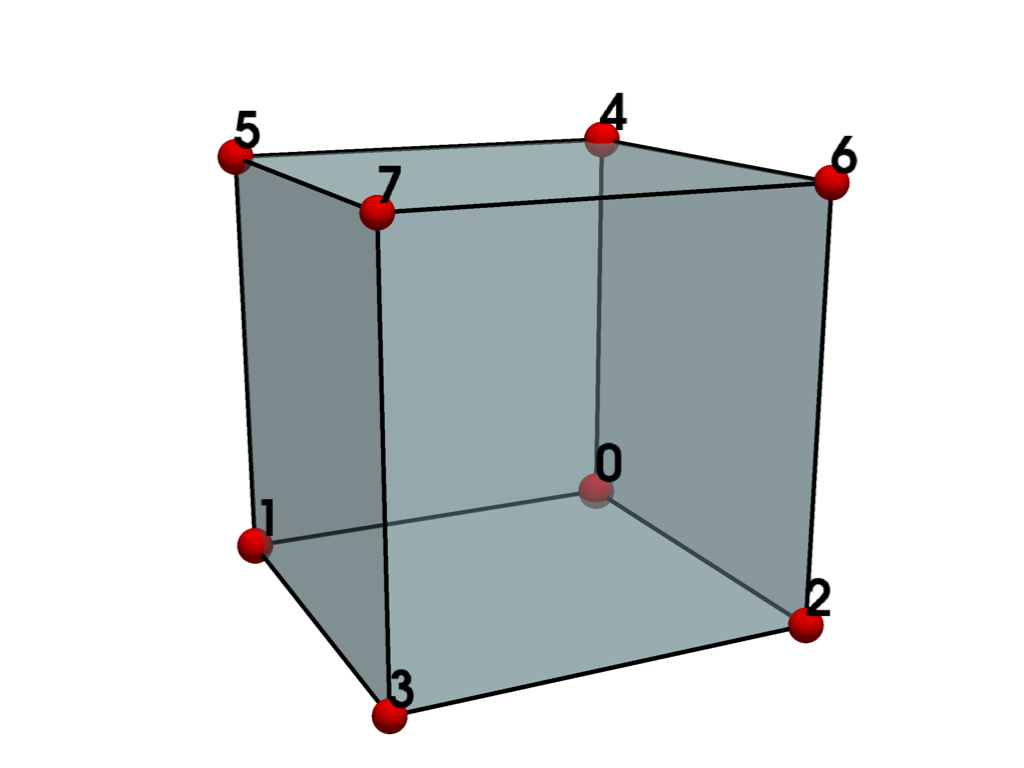
Linear Primary 3D Points: 8 Edges: 12 Faces: 6

Represents a 3D orthogonal parallelepiped.

The voxel is a primary three-dimensional cell defined by an ordered list of eight points.

Warning

This definition of a voxel differs from the conventional definition which describes a single constant-valued volume element. The meaning of this term can vary depending on context. See Image Data Representations for examples.

See also vtkVoxel.

HEXAHEDRON = <CellType.HEXAHEDRON: 12>#: pyvista.examples.cells.Hexahedron

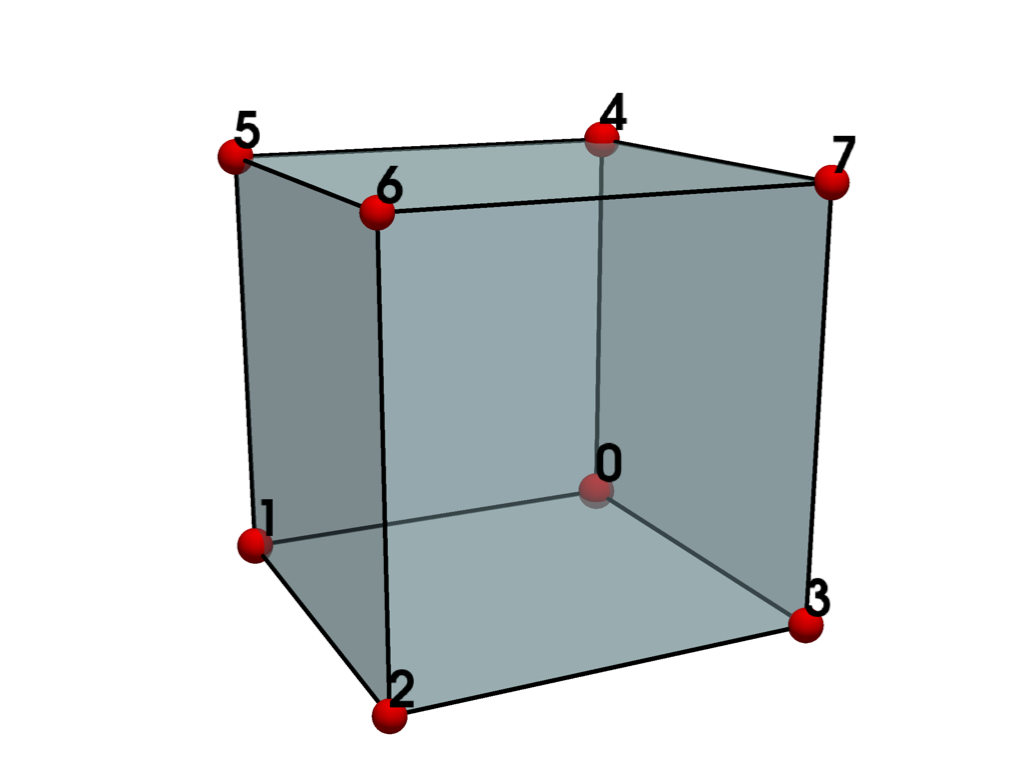
Linear Primary 3D Points: 8 Edges: 12 Faces: 6

Represents a 3D rectangular hexahedron.

The hexahedron is a primary three-dimensional cell consisting of six quadrilateral faces, twelve edges, and eight vertices.

See also vtkHexahedron.

WEDGE = <CellType.WEDGE: 13>#: pyvista.examples.cells.Wedge

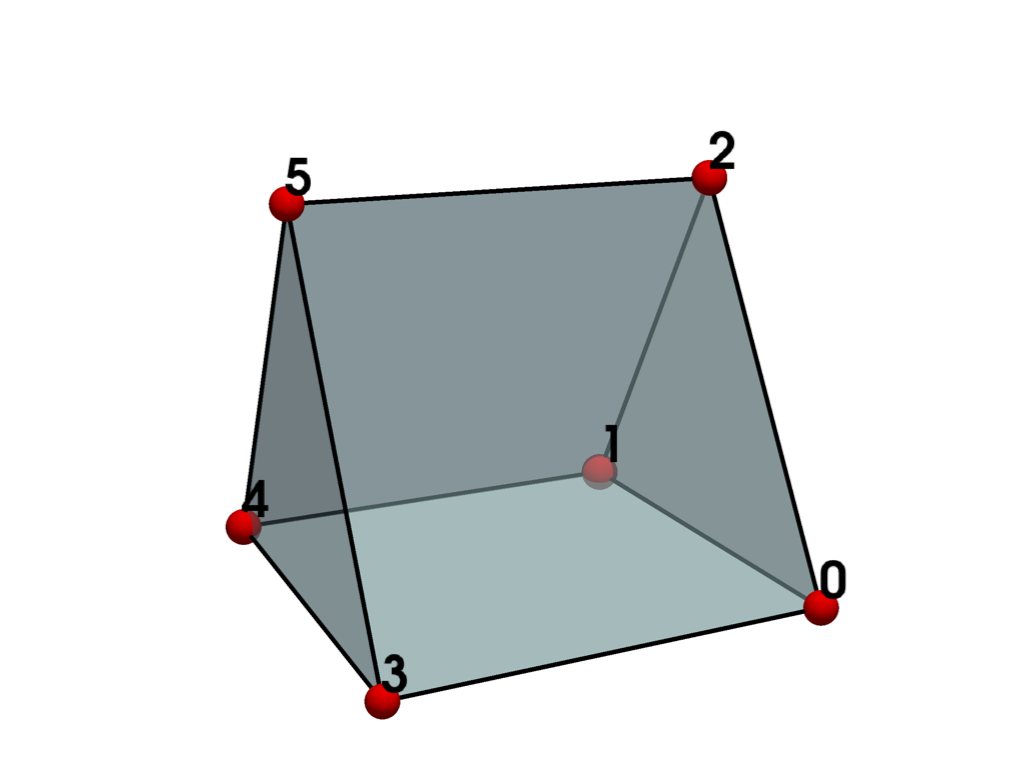
Linear Primary 3D Points: 6 Edges: 9 Faces: 5

Represents a linear 3D wedge.

The wedge is a primary three-dimensional cell consisting of two triangular and three quadrilateral faces.

See also vtkWedge.

PYRAMID = <CellType.PYRAMID: 14>#: pyvista.examples.cells.Pyramid

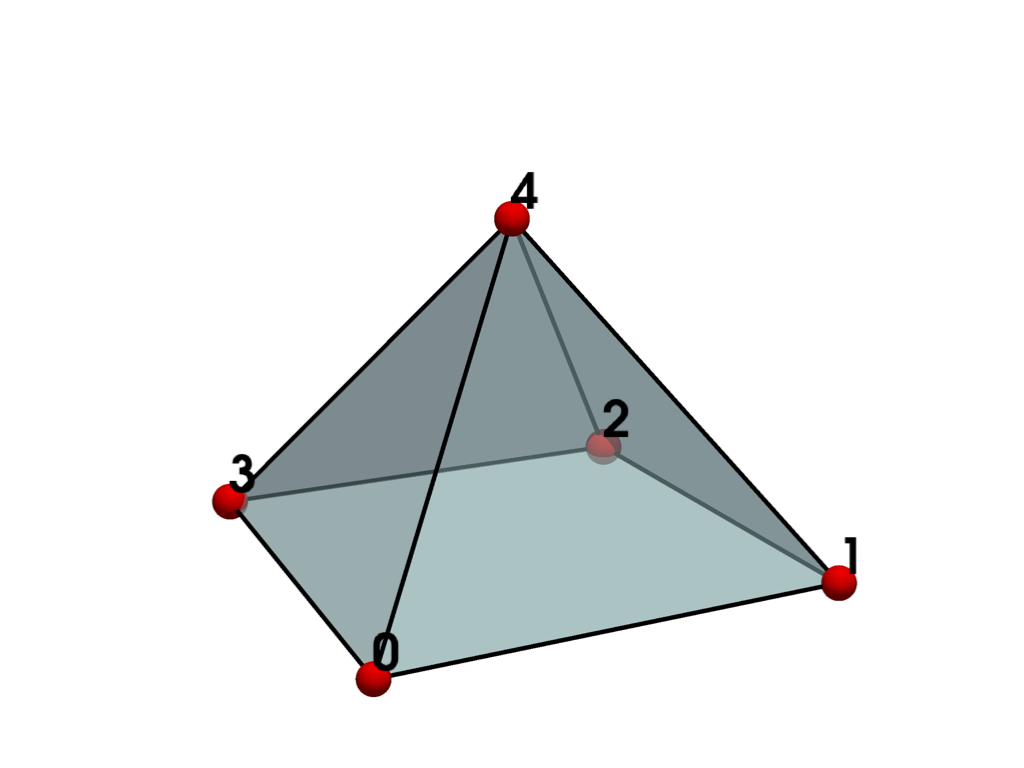
Linear Primary 3D Points: 5 Edges: 8 Faces: 5

Represents a 3D pyramid.

The pyramid is a primary three-dimensional cell consisting of a rectangular base with four triangular faces. It is defined by an ordered list of five points.

See also vtkPyramid.

PENTAGONAL_PRISM = <CellType.PENTAGONAL_PRISM: 15>#: pyvista.examples.cells.PentagonalPrism

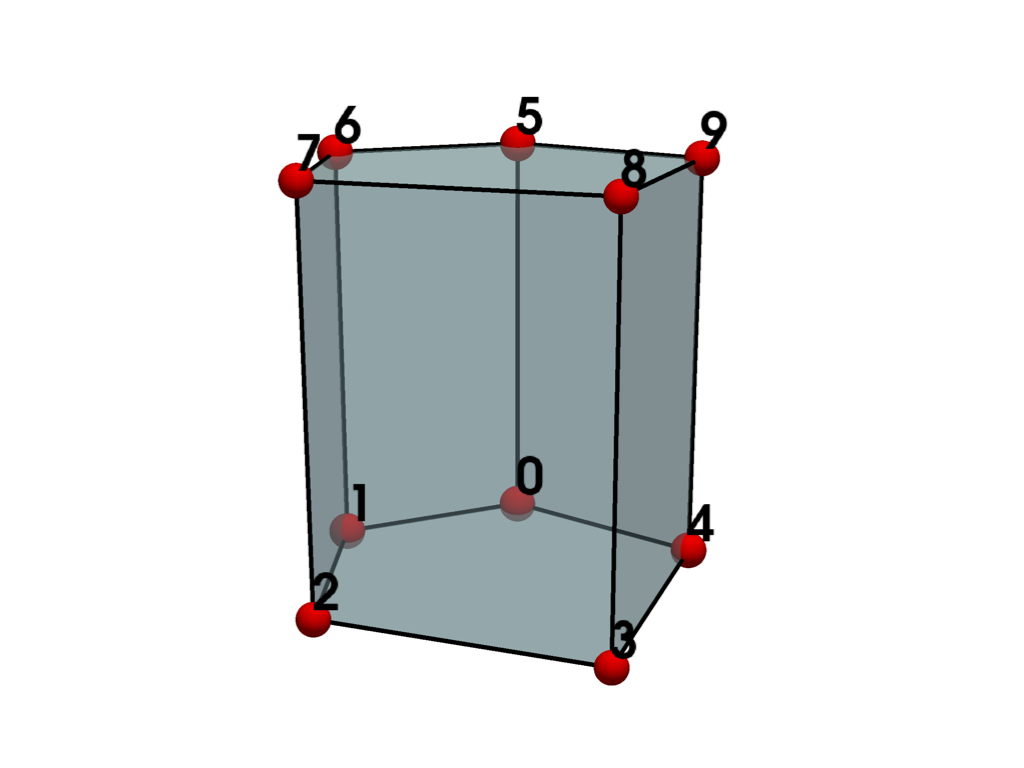
Linear Primary 3D Points: 10 Edges: 15 Faces: 7

Represents a convex 3D prism with a pentagonal base and five quadrilateral faces.

The pentagonal prism is a primary three-dimensional cell defined by an ordered list of ten points.

See also vtkPentagonalPrism.

HEXAGONAL_PRISM = <CellType.HEXAGONAL_PRISM: 16>#: pyvista.examples.cells.HexagonalPrism

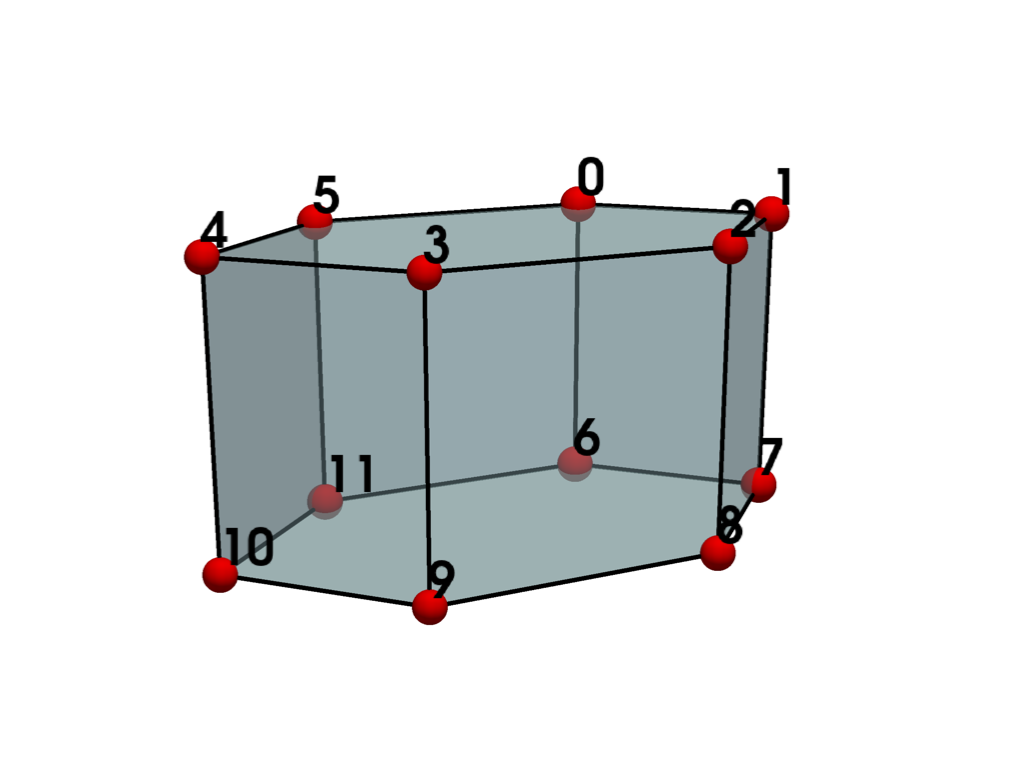
Linear Primary 3D Points: 12 Edges: 18 Faces: 8

Represents a 3D prism with hexagonal base and six quadrilateral faces.

The hexagonal prism is a primary three-dimensional cell defined by an ordered list of twelve points.

See also vtkHexagonalPrism.

QUADRATIC_EDGE = <CellType.QUADRATIC_EDGE: 21>#: pyvista.examples.cells.QuadraticEdge

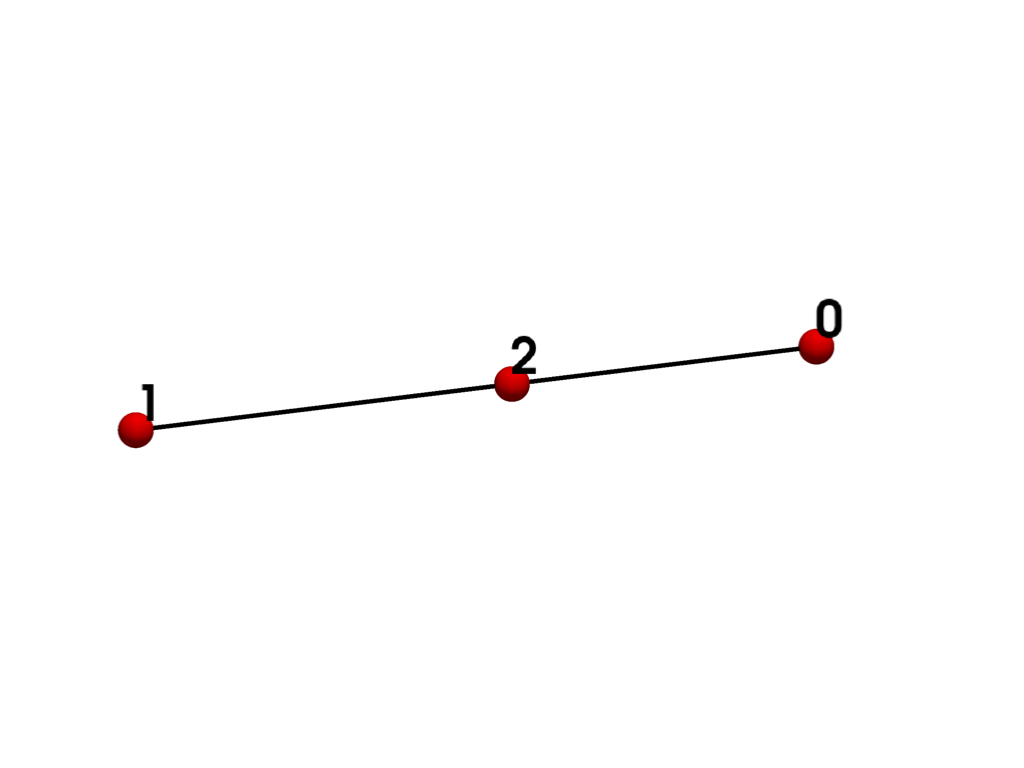
Non-linear Primary 1D Points: 3 Edges: 0 Faces: 0

Represents a 1D, 3-node, iso-parametric parabolic line.

The cell includes a mid-edge node.

See also vtkQuadraticEdge.

QUADRATIC_TRIANGLE = <CellType.QUADRATIC_TRIANGLE: 22>#: pyvista.examples.cells.QuadraticTriangle

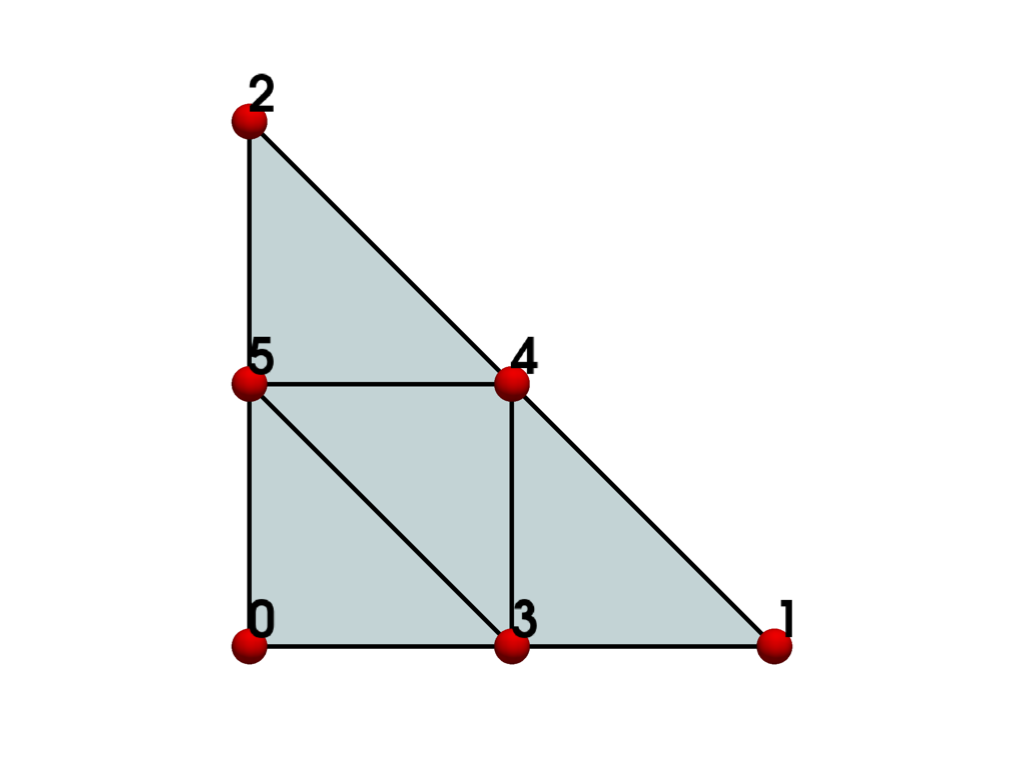
Non-linear Primary 2D Points: 6 Edges: 3 Faces: 0

Represents a 2D, 6-node, iso-parametric parabolic triangle.

The cell includes a mid-edge node for each of the three edges of the cell.

See also vtkQuadraticTriangle.

QUADRATIC_QUAD = <CellType.QUADRATIC_QUAD: 23>#: pyvista.examples.cells.QuadraticQuadrilateral

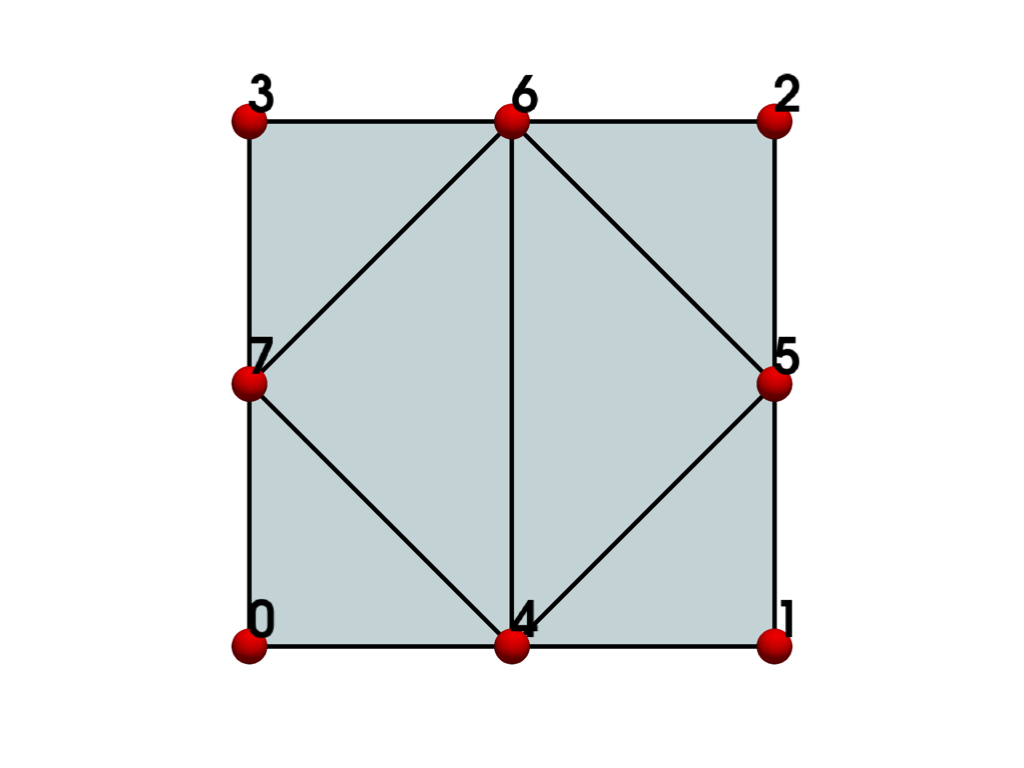
Non-linear Primary 2D Points: 8 Edges: 4 Faces: 0

Represents a 2D, 8-node iso-parametric parabolic quadrilateral element.

The cell includes a mid-edge node for each of the four edges of the cell.

See also vtkQuadraticQuad.

QUADRATIC_POLYGON = <CellType.QUADRATIC_POLYGON: 36>#: pyvista.examples.cells.QuadraticPolygon

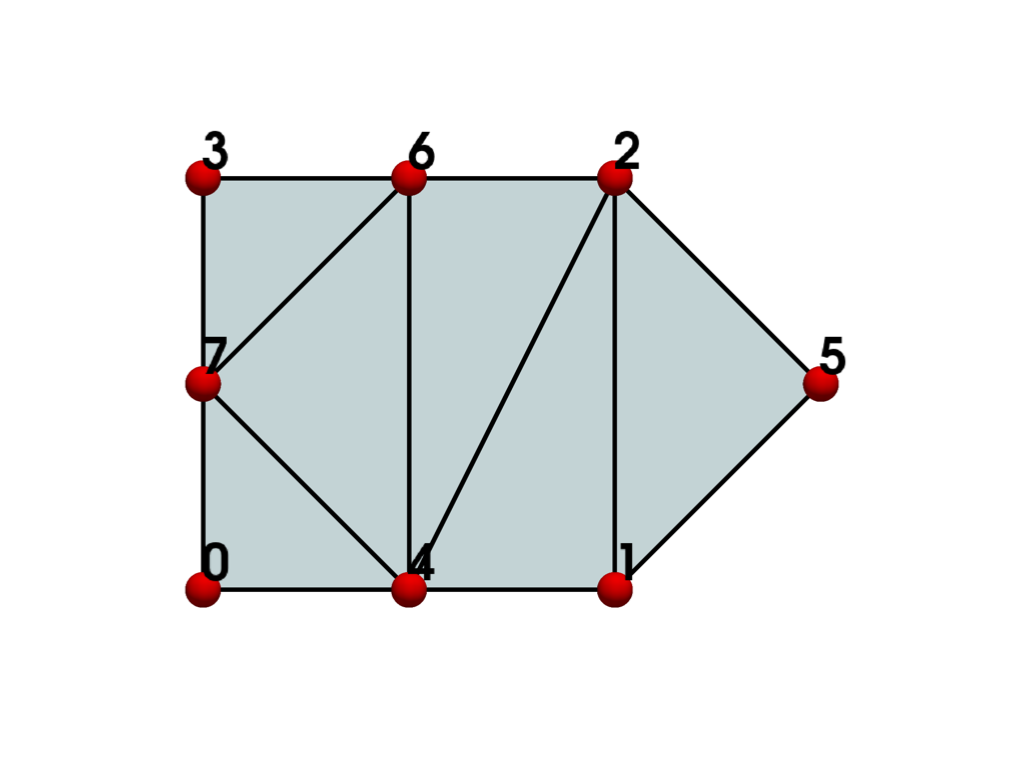
Non-linear Composite 2D Points: variable Edges: variable Faces: 0

Represents a 2D n-sided (2*n nodes) parabolic polygon.

The polygon cannot have any internal holes, and cannot self-intersect. The cell includes a mid-edge node for each of the n edges of the cell.

See also vtkQuadraticPolygon.

QUADRATIC_TETRA = <CellType.QUADRATIC_TETRA: 24>#: pyvista.examples.cells.QuadraticTetrahedron

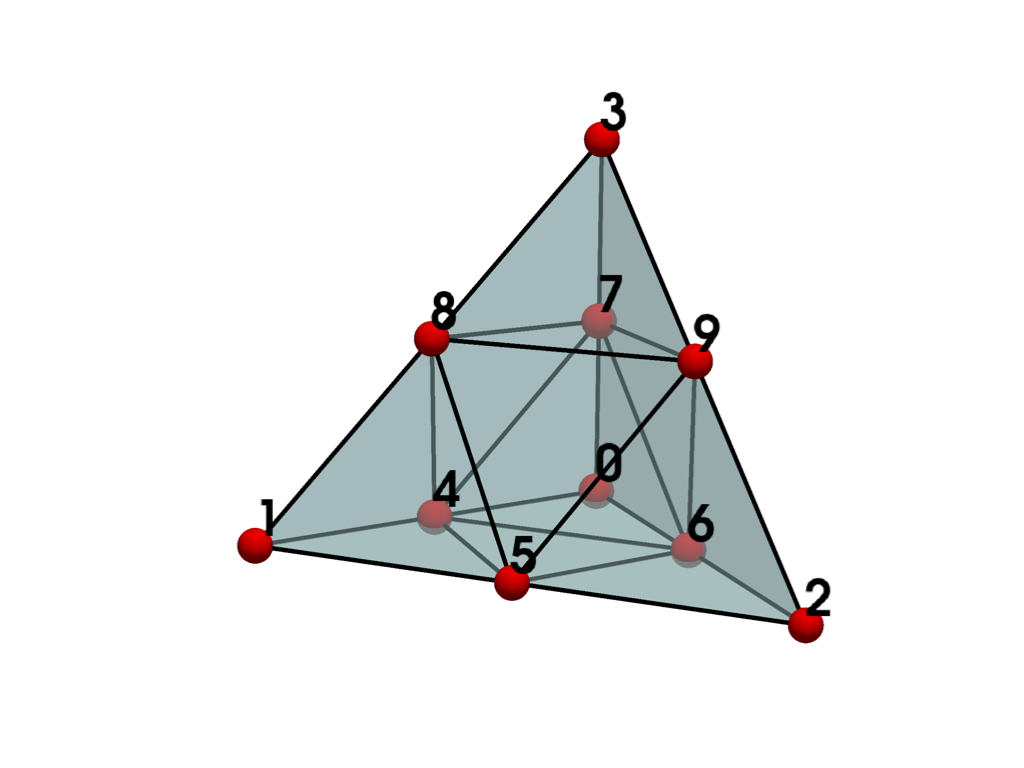
Non-linear Primary 3D Points: 10 Edges: 6 Faces: 4

Represents a 3D, 10-node, iso-parametric parabolic tetrahedron.

The cell includes a mid-edge node on each of the side edges of the tetrahedron.

See also vtkQuadraticTetra.

QUADRATIC_HEXAHEDRON = <CellType.QUADRATIC_HEXAHEDRON: 25>#: pyvista.examples.cells.QuadraticHexahedron

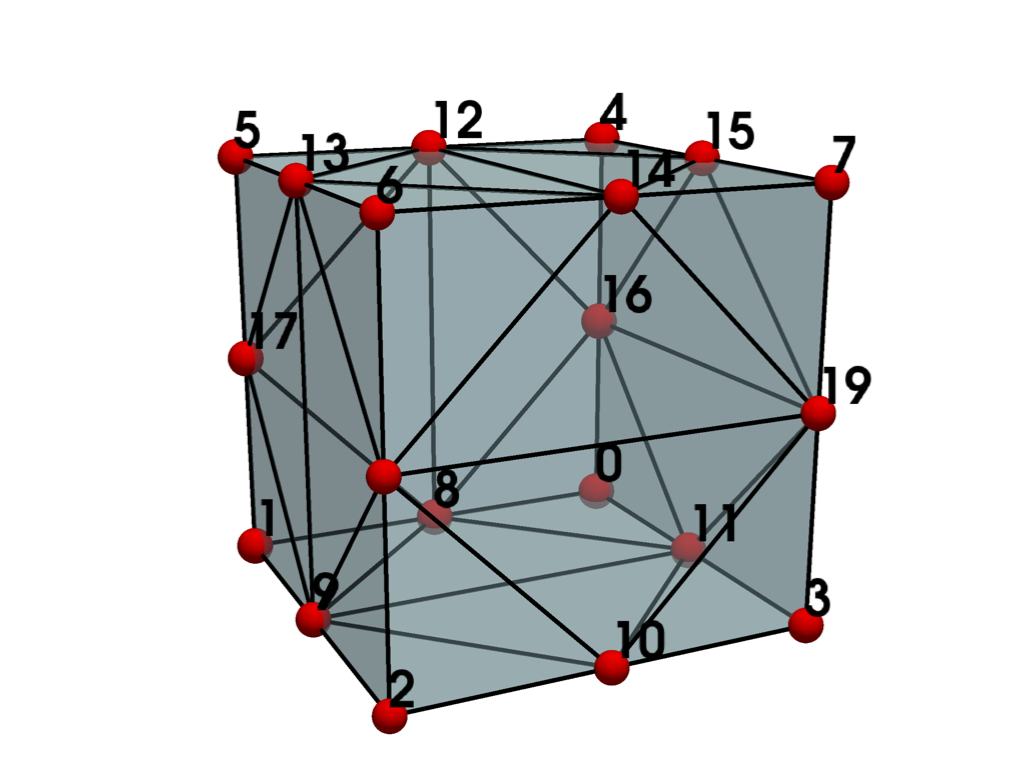
Non-linear Primary 3D Points: 20 Edges: 12 Faces: 6

Represents a 3D, 20-node iso-parametric parabolic hexahedron.

The cell includes a mid-edge node.

See also vtkQuadraticHexahedron.

QUADRATIC_WEDGE = <CellType.QUADRATIC_WEDGE: 26>#: pyvista.examples.cells.QuadraticWedge

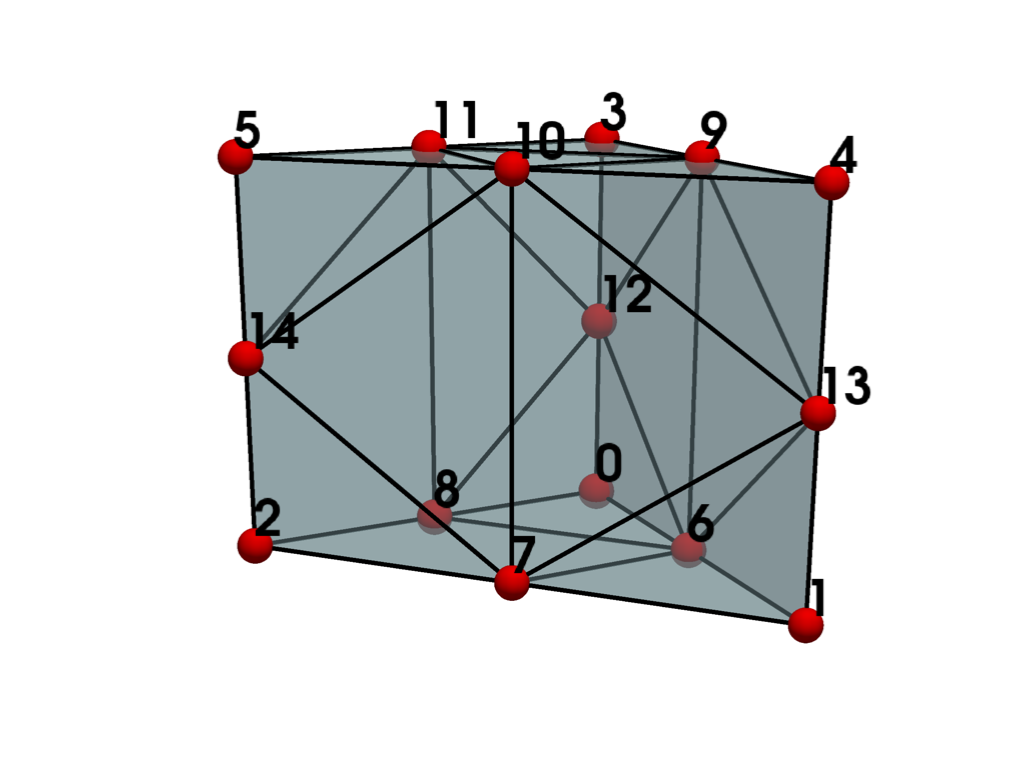
Non-linear Primary 3D Points: 15 Edges: 9 Faces: 5

Represents a 3D, 15-node iso-parametric parabolic wedge.

The cell includes a mid-edge node.

See also vtkQuadraticWedge.

QUADRATIC_PYRAMID = <CellType.QUADRATIC_PYRAMID: 27>#: pyvista.examples.cells.QuadraticPyramid

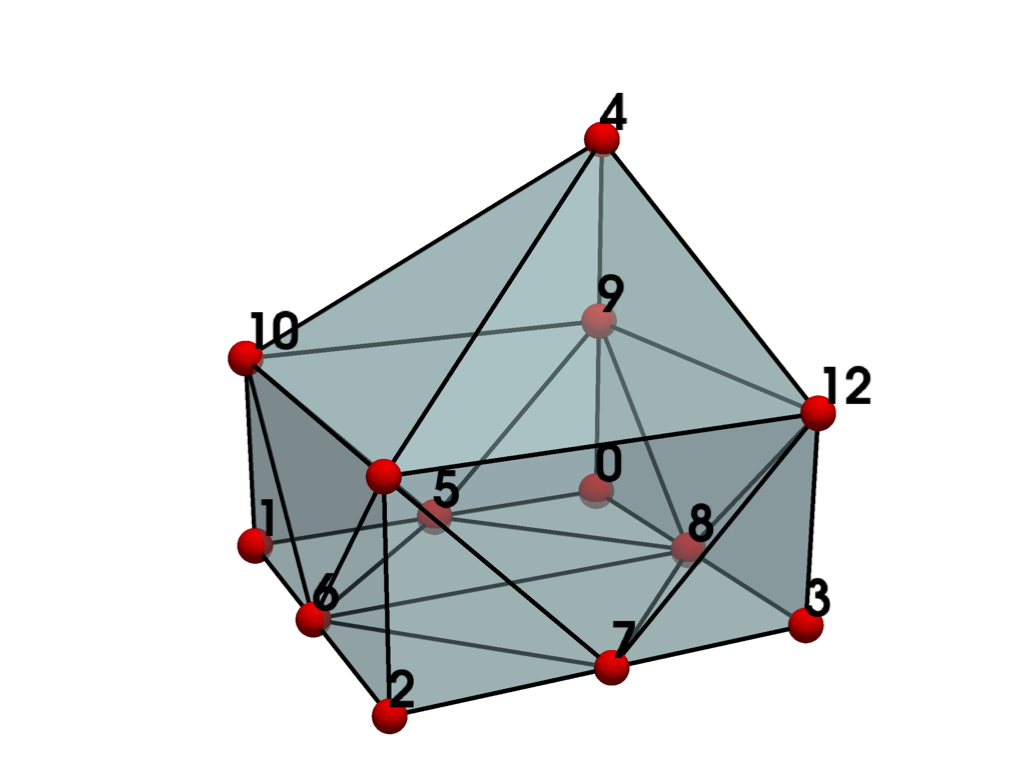
Non-linear Primary 3D Points: 13 Edges: 8 Faces: 5

Represents a 3D, 13-node iso-parametric parabolic pyramid.

The cell includes a mid-edge node.

See also vtkQuadraticPyramid.

BIQUADRATIC_QUAD = <CellType.BIQUADRATIC_QUAD: 28>#: pyvista.examples.cells.BiQuadraticQuadrilateral

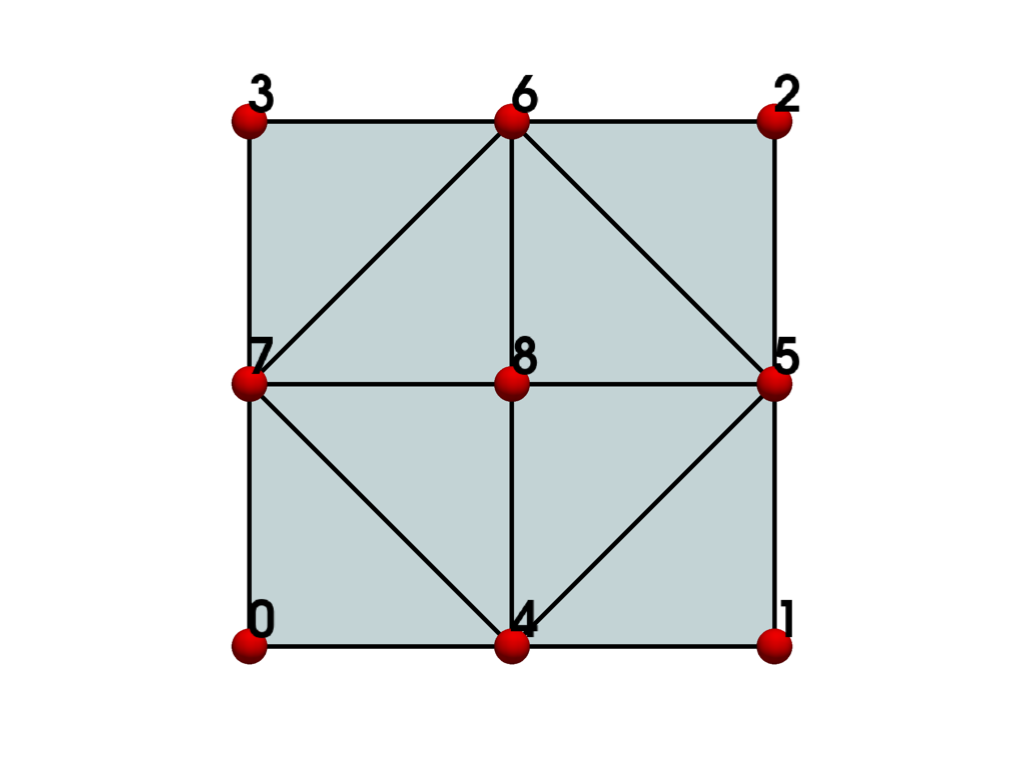
Non-linear Primary 2D Points: 9 Edges: 4 Faces: 0

Represents a 2D, 9-node iso-parametric parabolic quadrilateral element with a center-point.

The cell includes a mid-edge node for each of the four edges of the cell and a center node at the surface.

See also vtkBiQuadraticQuad.

TRIQUADRATIC_HEXAHEDRON = <CellType.TRIQUADRATIC_HEXAHEDRON: 29>#: pyvista.examples.cells.TriQuadraticHexahedron

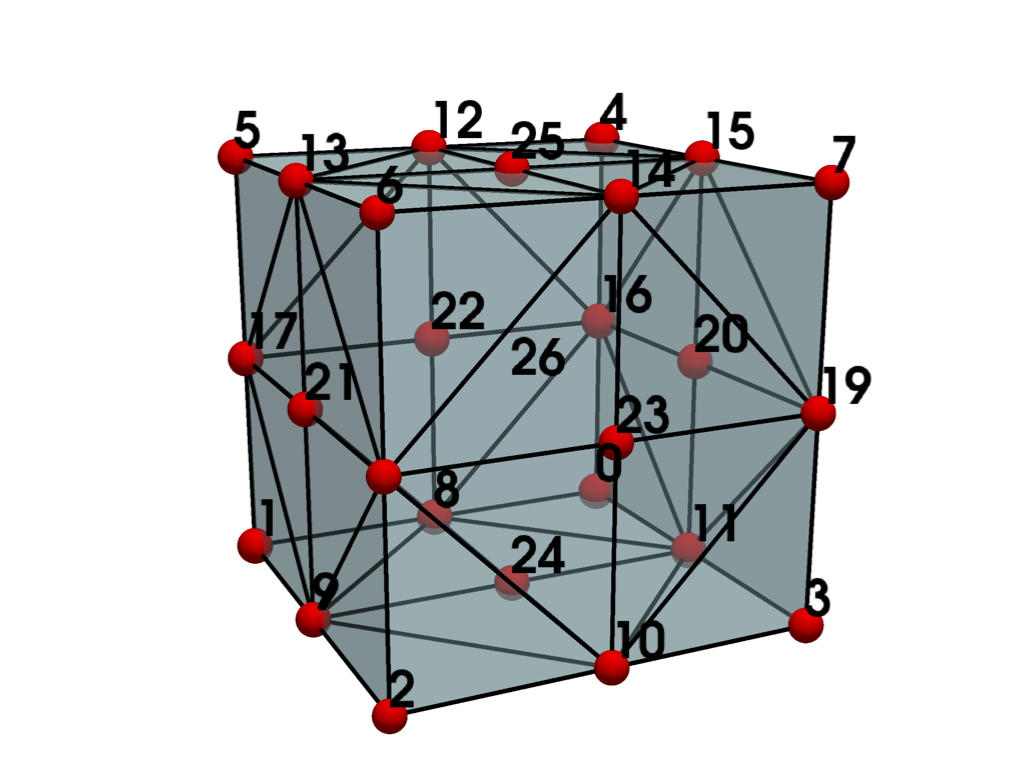
Non-linear Primary 3D Points: 27 Edges: 12 Faces: 6

Represents a 3D, 27-node iso-parametric triquadratic hexahedron.

The cell includes 8 edge nodes, 12 mid-edge nodes, 6 mid-face nodes and one mid-volume node.

See also vtkTriQuadraticHexahedron.

TRIQUADRATIC_PYRAMID = <CellType.TRIQUADRATIC_PYRAMID: 37>#: pyvista.examples.cells.TriQuadraticPyramid

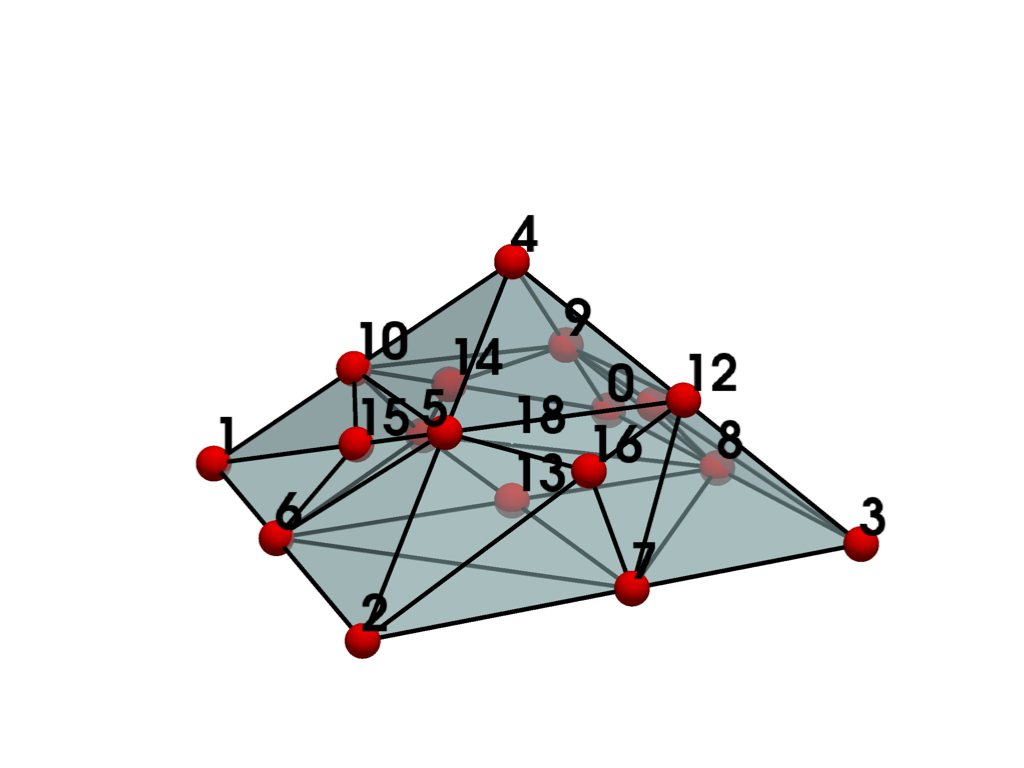
Non-linear Primary 3D Points: 19 Edges: 8 Faces: 5

Represents a second order 3D iso-parametric 19-node pyramid.

The cell includes 5 corner nodes, 8 mid-edge nodes, 5 mid-face nodes, and 1 volumetric centroid node.

See also vtkTriQuadraticPyramid.

QUADRATIC_LINEAR_QUAD = <CellType.QUADRATIC_LINEAR_QUAD: 30>#: pyvista.examples.cells.QuadraticLinearQuadrilateral

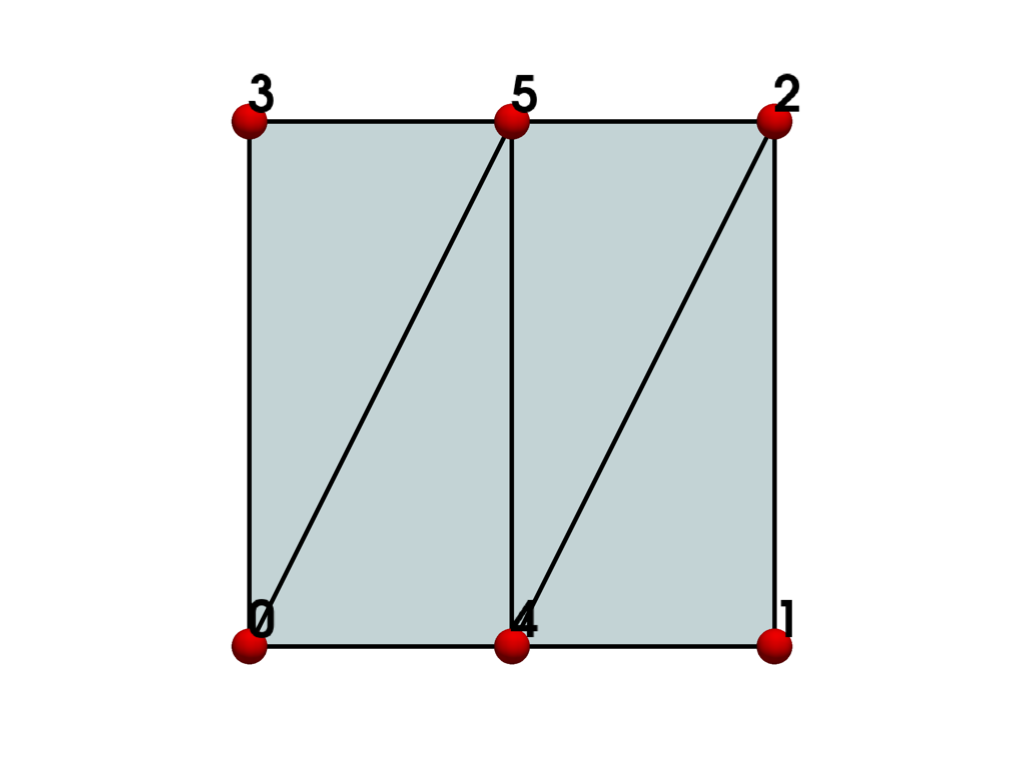
Non-linear Primary 2D Points: 6 Edges: 4 Faces: 0

Represents a 2D, 6-node iso-parametric quadratic-linear quadrilateral element.

The cell includes a mid-edge node for two of the four edges.

See also vtkQuadraticLinearQuad.

QUADRATIC_LINEAR_WEDGE = <CellType.QUADRATIC_LINEAR_WEDGE: 31>#: pyvista.examples.cells.QuadraticLinearWedge

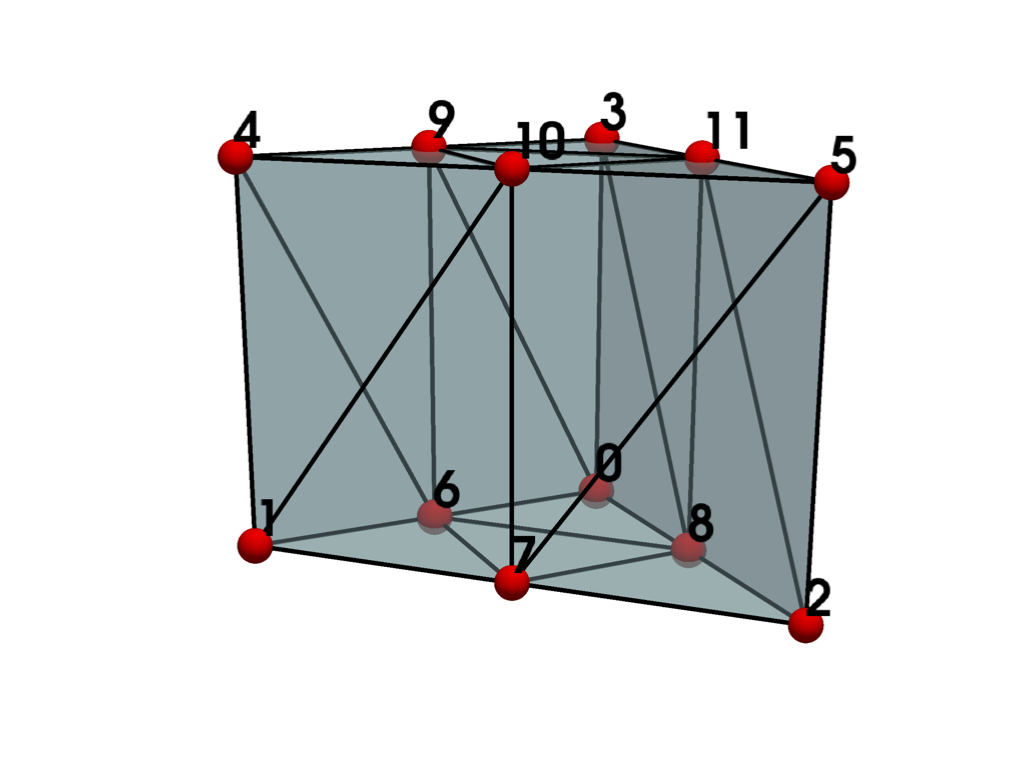
Non-linear Primary 3D Points: 12 Edges: 9 Faces: 5

Represents a 3D, 12-node iso-parametric linear quadratic wedge.

The cell includes mid-edge node in the triangle edges.

See also vtkQuadraticLinearWedge.

BIQUADRATIC_QUADRATIC_WEDGE = <CellType.BIQUADRATIC_QUADRATIC_WEDGE: 32>#: pyvista.examples.cells.BiQuadraticQuadraticWedge

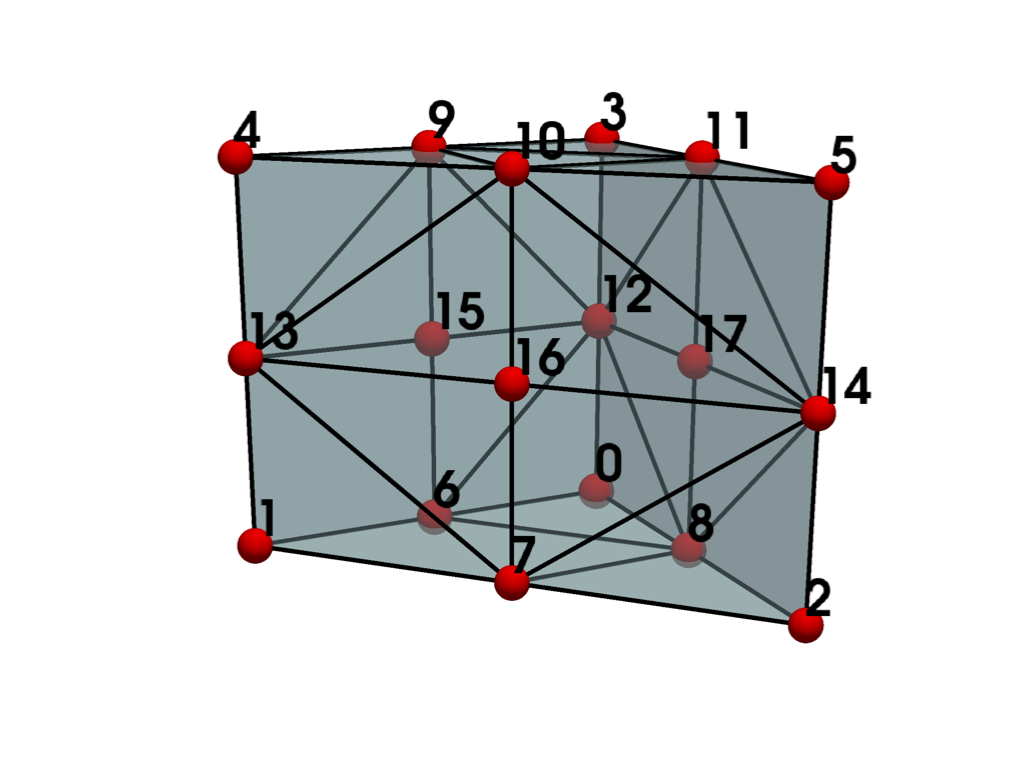
Non-linear Primary 3D Points: 18 Edges: 9 Faces: 5

Represents a 3D, 18-node iso-parametric bi-quadratic wedge.

The cell includes a mid-edge node.

See also vtkBiQuadraticQuadraticWedge.

BIQUADRATIC_QUADRATIC_HEXAHEDRON = <CellType.BIQUADRATIC_QUADRATIC_HEXAHEDRON: 33>#: pyvista.examples.cells.BiQuadraticQuadraticHexahedron

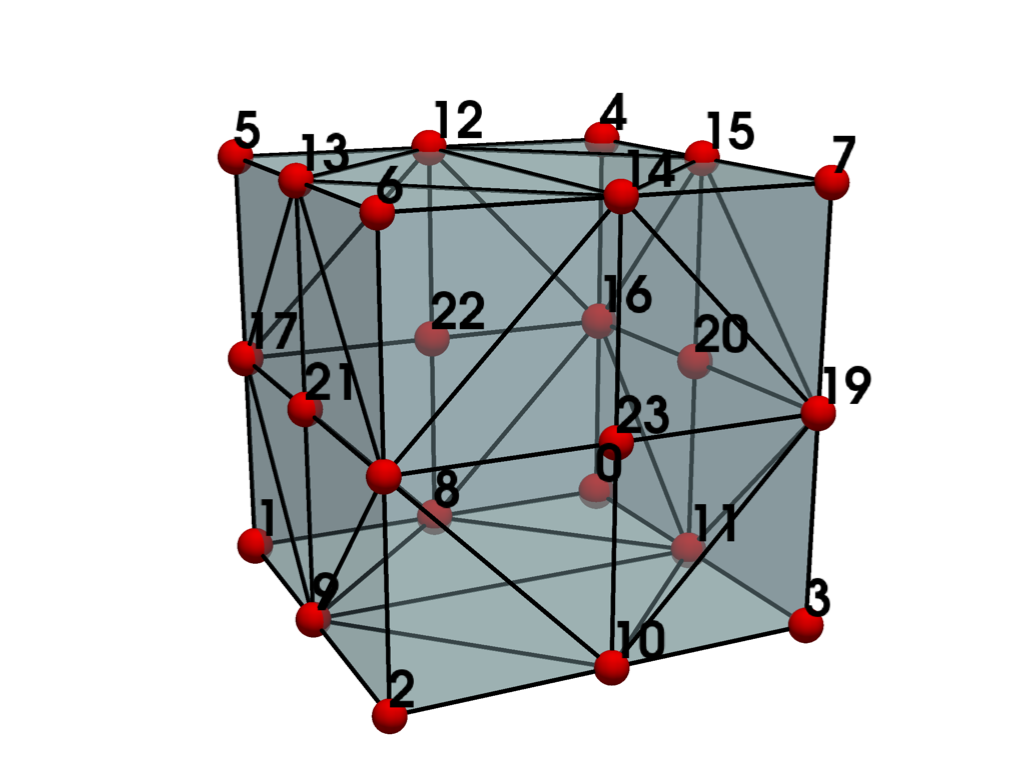
Non-linear Primary 3D Points: 24 Edges: 12 Faces: 6

Represents a 3D, 24-node iso-parametric biquadratic hexahedron.

The cell includes mid-edge and center-face nodes.

See also vtkBiQuadraticQuadraticHexahedron.

BIQUADRATIC_TRIANGLE = <CellType.BIQUADRATIC_TRIANGLE: 34>#: pyvista.examples.cells.BiQuadraticTriangle

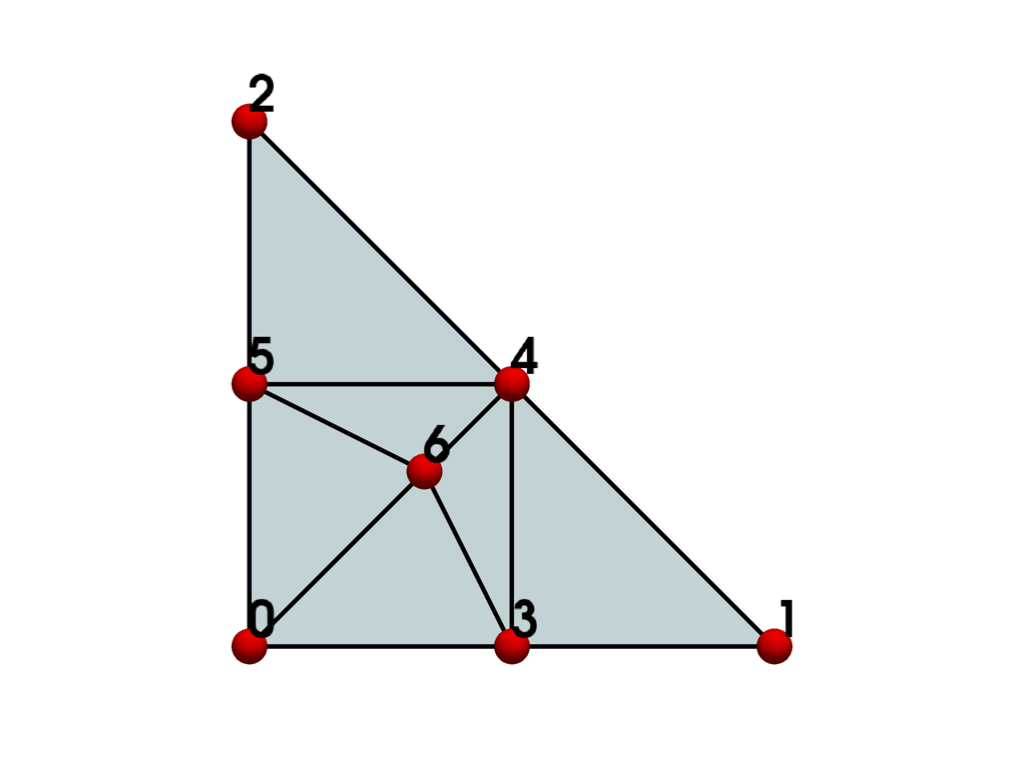
Non-linear Primary 2D Points: 7 Edges: 3 Faces: 0

Represents a 2D, 7-node, iso-parametric parabolic triangle.

The cell includes three mid-edge nodes besides the three triangle vertices and a center node.

See also vtkBiQuadraticTriangle.

CUBIC_LINE = <CellType.CUBIC_LINE: 35>#: pyvista.examples.cells.CubicLine

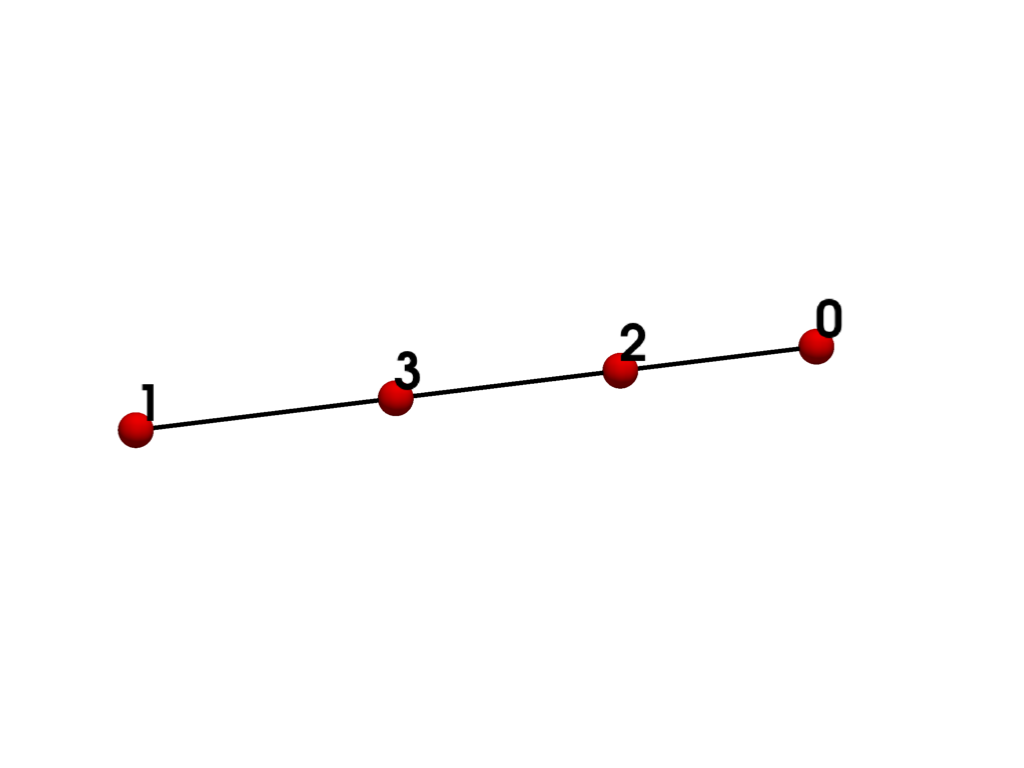
Non-linear Primary 1D Points: 4 Edges: 0 Faces: 0

Represents a 1D iso-parametric cubic line.

The cell includes two mid-edge nodes.

See also vtkCubicLine.

CONVEX_POINT_SET = <CellType.CONVEX_POINT_SET: 41>#: Linear Composite 3D Points: variable Edges: 0 Faces: 0

See also vtkConvexPointSet.

POLYHEDRON = <CellType.POLYHEDRON: 42>#: pyvista.examples.cells.Polyhedron

Linear Primary 3D Points: variable Edges: variable Faces: variable

Represents a 3D cell defined by a set of polygonal faces.

See also vtkPolyhedron.

PARAMETRIC_CURVE = <CellType.PARAMETRIC_CURVE: 51>#

PARAMETRIC_SURFACE = <CellType.PARAMETRIC_SURFACE: 52>#

PARAMETRIC_TRI_SURFACE = <CellType.PARAMETRIC_TRI_SURFACE: 53>#

PARAMETRIC_QUAD_SURFACE = <CellType.PARAMETRIC_QUAD_SURFACE: 54>#

PARAMETRIC_TETRA_REGION = <CellType.PARAMETRIC_TETRA_REGION: 55>#

PARAMETRIC_HEX_REGION = <CellType.PARAMETRIC_HEX_REGION: 56>#

HIGHER_ORDER_EDGE = <CellType.HIGHER_ORDER_EDGE: 60>#

HIGHER_ORDER_TRIANGLE = <CellType.HIGHER_ORDER_TRIANGLE: 61>#

HIGHER_ORDER_QUAD = <CellType.HIGHER_ORDER_QUAD: 62>#

HIGHER_ORDER_POLYGON = <CellType.HIGHER_ORDER_POLYGON: 63>#

HIGHER_ORDER_TETRAHEDRON = <CellType.HIGHER_ORDER_TETRAHEDRON: 64>#

HIGHER_ORDER_WEDGE = <CellType.HIGHER_ORDER_WEDGE: 65>#

HIGHER_ORDER_PYRAMID = <CellType.HIGHER_ORDER_PYRAMID: 66>#

HIGHER_ORDER_HEXAHEDRON = <CellType.HIGHER_ORDER_HEXAHEDRON: 67>#

LAGRANGE_CURVE = <CellType.LAGRANGE_CURVE: 68>#: Non-linear Primary 1D Points: 2 Edges: 0 Faces: 0

See also vtkLagrangeCurve.

LAGRANGE_TRIANGLE = <CellType.LAGRANGE_TRIANGLE: 69>#: Non-linear Primary 2D Points: 3 Edges: 3 Faces: 0

See also vtkLagrangeTriangle.

LAGRANGE_QUADRILATERAL = <CellType.LAGRANGE_QUADRILATERAL: 70>#: Non-linear Primary 2D Points: 4 Edges: 4 Faces: 0

See also vtkLagrangeQuadrilateral.

LAGRANGE_TETRAHEDRON = <CellType.LAGRANGE_TETRAHEDRON: 71>#

LAGRANGE_HEXAHEDRON = <CellType.LAGRANGE_HEXAHEDRON: 72>#: Non-linear Primary 3D Points: 8 Edges: 12 Faces: 6

See also vtkLagrangeHexahedron.

LAGRANGE_WEDGE = <CellType.LAGRANGE_WEDGE: 73>#: Non-linear Primary 3D Points: 6 Edges: 9 Faces: 5

See also vtkLagrangeWedge.

LAGRANGE_PYRAMID = <CellType.LAGRANGE_PYRAMID: 74>#

BEZIER_CURVE = <CellType.BEZIER_CURVE: 75>#: Non-linear Primary 1D Points: 2 Edges: 0 Faces: 0

See also vtkBezierCurve.

BEZIER_TRIANGLE = <CellType.BEZIER_TRIANGLE: 76>#: Non-linear Primary 2D Points: 3 Edges: 3 Faces: 0

See also vtkBezierTriangle.

BEZIER_QUADRILATERAL = <CellType.BEZIER_QUADRILATERAL: 77>#: Non-linear Primary 2D Points: 4 Edges: 4 Faces: 0

See also vtkBezierQuadrilateral.

BEZIER_TETRAHEDRON = <CellType.BEZIER_TETRAHEDRON: 78>#: Non-linear Primary 3D Points: 4 Edges: 6 Faces: 4

See also vtkBezierTetra.

BEZIER_HEXAHEDRON = <CellType.BEZIER_HEXAHEDRON: 79>#: Non-linear Primary 3D Points: 8 Edges: 12 Faces: 6

See also vtkBezierHexahedron.

BEZIER_WEDGE = <CellType.BEZIER_WEDGE: 80>#: Non-linear Primary 3D Points: 6 Edges: 9 Faces: 5

See also vtkBezierWedge.

BEZIER_PYRAMID = <CellType.BEZIER_PYRAMID: 81>#

pyvista.CellType

Contents

pyvista.CellType#