Plotting Bounds

This example demonstrates to show bounds within a pyvista.Plotter using show_grid()

from __future__ import annotations

import pyvista as pv
from pyvista import examples

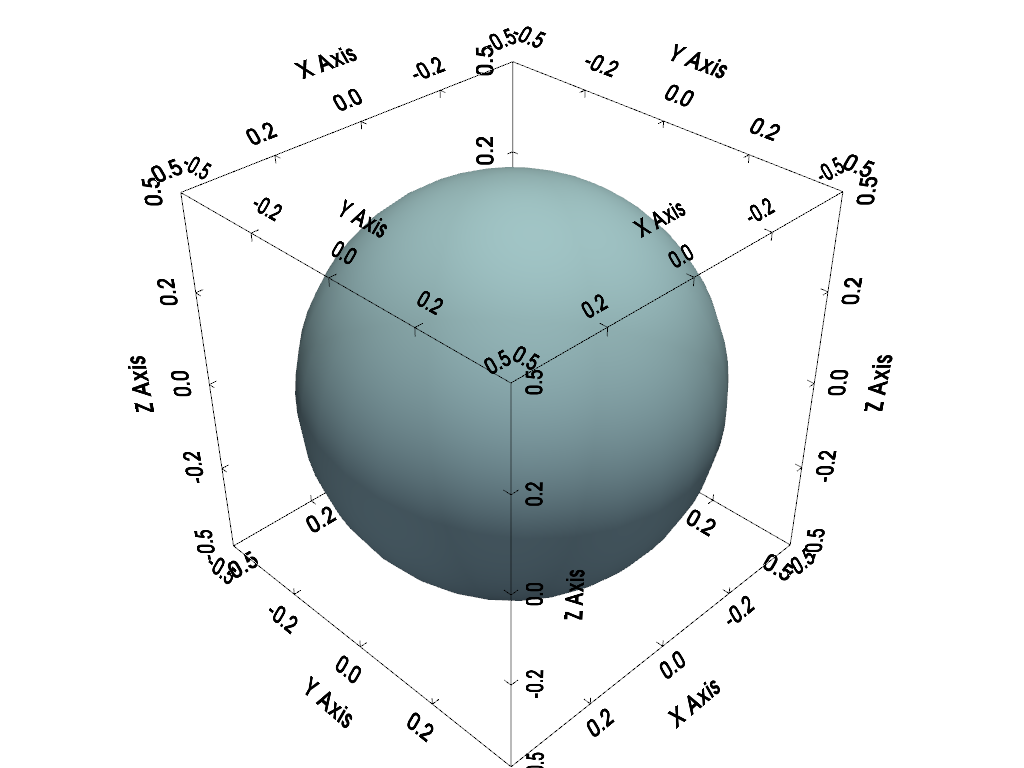
Show All Bounds

In this plot we show the bounds for all axes by setting location='all'.

plotter = pv.Plotter()
plotter.add_mesh(pv.Sphere(), smooth_shading=True)
plotter.show_bounds(location='all')
plotter.show()

Static Scene

Interactive Scene

Override Shown Values Limits

In this example, we override the values shown along the X and Y axes with our own custom values. This can be useful when you wish to display different values along the axes without having to scale the dataset. Also, note how we hide the Z labels by setting show_zlabels=False.

gears = examples.download_gears()

plotter = pv.Plotter()
plotter.add_mesh(gears, smooth_shading=True, split_sharp_edges=True)
plotter.show_bounds(axes_ranges=[0, 5, 0, 5, 0, 2], show_zlabels=False)
plotter.show()

print(f'Actual dataset bounds: {gears.bounds}')

Static Scene

Interactive Scene

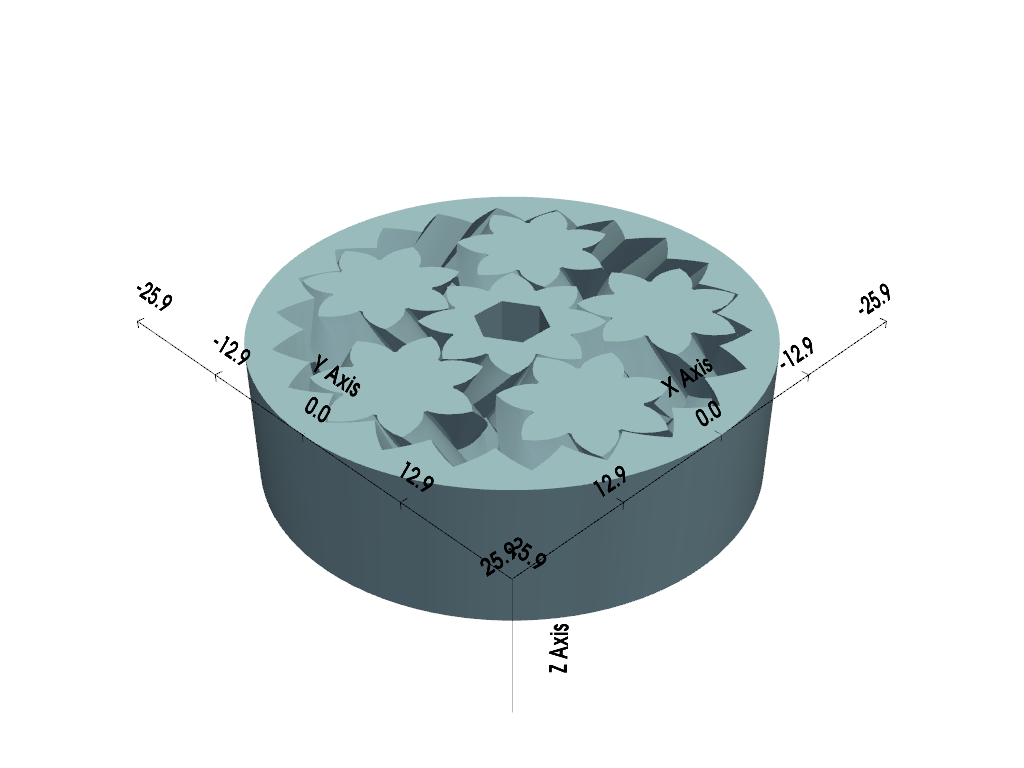
Actual dataset bounds: BoundsTuple(x_min=-25.850000381469727, x_max=25.850000381469727, y_min=-25.850000381469727, y_max=25.850000381469727, z_min=0.0, z_max=15.0)

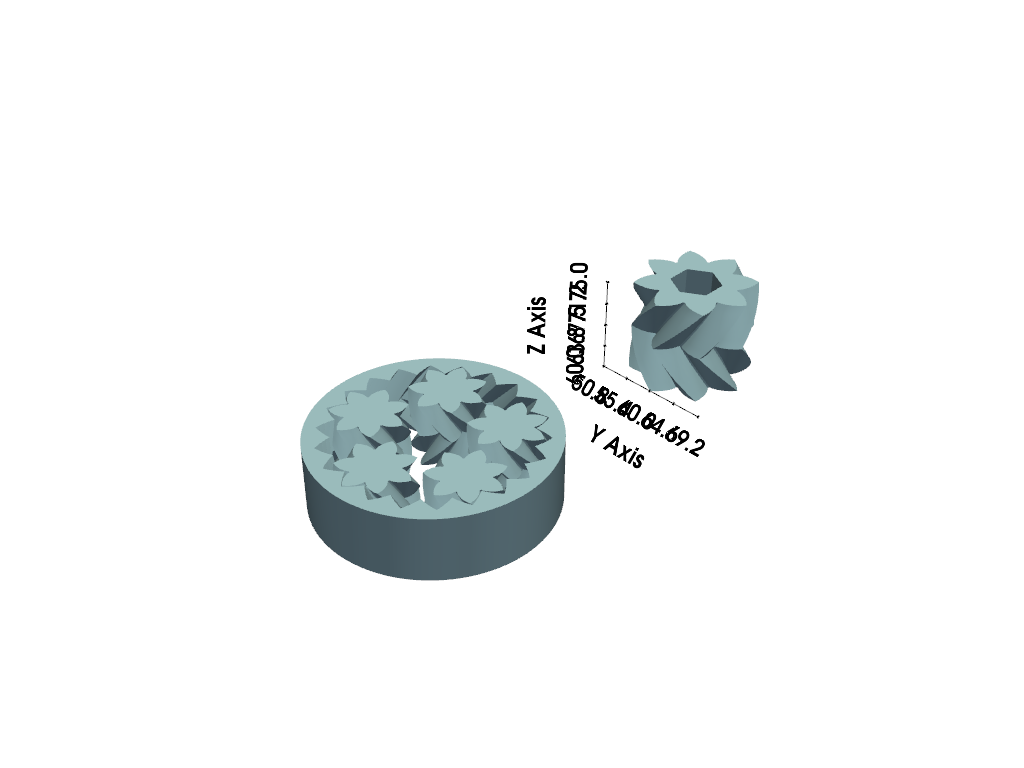
Show Bounds for Only One Dataset

This example shows only the bounds for a single dataset. Again we use axes_ranges here since in this example we want to show the size of the single central gear.

# separate and shift the central gear
split_gears = gears.split_bodies()
central_gear = split_gears.pop(1)
central_gear.translate([0, 60, 60], inplace=True)

# also, grab the size of the central gear
bnds = central_gear.bounds
x_size = bnds.x_max - bnds.x_min
y_size = bnds.y_max - bnds.y_min
z_size = bnds.z_max - bnds.z_min

plotter = pv.Plotter()
plotter.add_mesh(split_gears, smooth_shading=True, split_sharp_edges=True)
plotter.add_mesh(central_gear, smooth_shading=True, split_sharp_edges=True)
plotter.show_grid(
    mesh=central_gear,
    axes_ranges=[0, x_size, 0, y_size, 0, z_size],
    show_xaxis=False,
    bold=True,
    grid=False,
)
plotter.show()

Static Scene

Interactive Scene

Tags: plot