Note
Go to the end to download the full example code.
Display Eigenmodes of Vibration#
This example applies the warp_by_vector filter to a cube whose eigenmodes have
been computed using the Ritz method, as outlined in Visscher, William M.,
Albert Migliori, Thomas M. Bell, et Robert A. Reinert. “On the normal modes of
free vibration of inhomogeneous and anisotropic elastic objects”. The Journal
of the Acoustical Society of America 90, n.4 (October 1991): 2154-62.
https://asa.scitation.org/doi/10.1121/1.401643.
First, let’s solve the eigenvalue problem for a vibrating cube. We use a crude approximation (by choosing a low max polynomial order) to get a fast computation.
from __future__ import annotations
from itertools import product
import numpy as np
from scipy.linalg import eigh
import pyvista as pv
def analytical_integral_rppd(p, q, r, a, b, c):
"""Return the analytical value of the RPPD integral.
This is the integral of x**p * y**q * z**r for (x, -a, a), (y, -b, b), (z, -c, c).
"""
if p < 0 or q < 0 or r < 0.0:
return 0.0
else:
return (
a ** (p + 1)
* b ** (q + 1)
* c ** (r + 1)
* ((-1) ** p + 1)
* ((-1) ** q + 1)
* ((-1) ** r + 1)
/ ((p + 1) * (q + 1) * (r + 1))
)
def make_cijkl_E_nu(E=200, nu=0.3):
"""
Make cijkl from E and nu.
Default values for steel are: E=200 GPa, nu=0.3.
"""
lambd = E * nu / (1 + nu) / (1 - 2 * nu)
mu = E / 2 / (1 + nu)
cij = np.zeros((6, 6))
cij[(0, 1, 2), (0, 1, 2)] = lambd + 2 * mu
cij[(0, 0, 1, 1, 2, 2), (1, 2, 0, 2, 0, 1)] = lambd
cij[(3, 4, 5), (3, 4, 5)] = mu
# check symmetry
assert np.allclose(cij, cij.T)
# convert to order 4 tensor
coord_mapping = {
(1, 1): 1,
(2, 2): 2,
(3, 3): 3,
(2, 3): 4,
(1, 3): 5,
(1, 2): 6,
(2, 1): 6,
(3, 1): 5,
(3, 2): 4,
}
cijkl = np.zeros((3, 3, 3, 3))
for i, j, k, l in product(range(3), repeat=4):
u = coord_mapping[i + 1, j + 1]
v = coord_mapping[k + 1, l + 1]
cijkl[i, j, k, l] = cij[u - 1, v - 1]
return cijkl, cij
def get_first_N_above_thresh(N, freqs, thresh, decimals=3):
"""Return first N unique frequencies with amplitude above threshold based on first decimals."""
unique_freqs, unique_indices = np.unique(np.round(freqs, decimals=decimals), return_index=True)
nonzero = unique_freqs > thresh
unique_freqs, unique_indices = unique_freqs[nonzero], unique_indices[nonzero]
return unique_freqs[:N], unique_indices[:N]
def assemble_mass_and_stiffness(N, F, geom_params, cijkl):
"""
Assemble the mass and stiffness matrix.
It first builds an index of basis functions as a quadruplet of
component and polynomial order for (x^p, y^q, z^r) of maximum order N.
This routine only builds the symmetric part of the matrix to speed
things up.
"""
# building coordinates
triplets = [
(p, q, r) for p in range(N + 1) for q in range(N - p + 1) for r in range(N - p - q + 1)
]
assert len(triplets) == (N + 1) * (N + 2) * (N + 3) // 6
quadruplets = []
for i, triplet in product(range(3), triplets):
quadruplets.append((i, *triplet))
assert len(quadruplets) == 3 * (N + 1) * (N + 2) * (N + 3) // 6
# assembling the mass and stiffness matrix in a single loop
R = len(triplets)
E = np.zeros((3 * R, 3 * R)) # the mass matrix
G = np.zeros((3 * R, 3 * R)) # the stiffness matrix
for index1, quad1 in enumerate(quadruplets):
I, p1, q1, r1 = quad1
for index2, quad2 in enumerate(quadruplets[index1:]):
index2 = index2 + index1
J, p2, q2, r2 = quad2
G[index1, index2] = (
cijkl[I, 1 - 1, J, 1 - 1]
* p1
* p2
* F(p1 + p2 - 2, q1 + q2, r1 + r2, **geom_params)
+ cijkl[I, 1 - 1, J, 2 - 1]
* p1
* q2
* F(p1 + p2 - 1, q1 + q2 - 1, r1 + r2, **geom_params)
+ cijkl[I, 1 - 1, J, 3 - 1]
* p1
* r2
* F(p1 + p2 - 1, q1 + q2, r1 + r2 - 1, **geom_params)
+ cijkl[I, 2 - 1, J, 1 - 1]
* q1
* p2
* F(p1 + p2 - 1, q1 + q2 - 1, r1 + r2, **geom_params)
+ cijkl[I, 2 - 1, J, 2 - 1]
* q1
* q2
* F(p1 + p2, q1 + q2 - 2, r1 + r2, **geom_params)
+ cijkl[I, 2 - 1, J, 3 - 1]
* q1
* r2
* F(p1 + p2, q1 + q2 - 1, r1 + r2 - 1, **geom_params)
+ cijkl[I, 3 - 1, J, 1 - 1]
* r1
* p2
* F(p1 + p2 - 1, q1 + q2, r1 + r2 - 1, **geom_params)
+ cijkl[I, 3 - 1, J, 2 - 1]
* r1
* q2
* F(p1 + p2, q1 + q2 - 1, r1 + r2 - 1, **geom_params)
+ cijkl[I, 3 - 1, J, 3 - 1]
* r1
* r2
* F(p1 + p2, q1 + q2, r1 + r2 - 2, **geom_params)
)
G[index2, index1] = G[index1, index2] # since stiffness matrix is symmetric
if I == J:
E[index1, index2] = F(p1 + p2, q1 + q2, r1 + r2, **geom_params)
E[index2, index1] = E[index1, index2] # since mass matrix is symmetric
return E, G, quadruplets
N = 8 # maximum order of x^p y^q z^r polynomials
rho = 8.0 # g/cm^3
l1, l2, l3 = 0.2, 0.2, 0.2 # all in cm
geometry_parameters = {'a': l1 / 2.0, 'b': l2 / 2.0, 'c': l3 / 2.0}
cijkl, cij = make_cijkl_E_nu(200, 0.3) # Gpa, without unit
E, G, quadruplets = assemble_mass_and_stiffness(
N,
analytical_integral_rppd,
geometry_parameters,
cijkl,
)
# solving the eigenvalue problem using symmetric solver
w, vr = eigh(a=G, b=E)
omegas = np.sqrt(np.abs(w) / rho) * 1e5 # convert back to Hz
freqs = omegas / (2 * np.pi)
# expected values from (Bernard 2014, p.14),
# error depends on polynomial order ``N``
expected_freqs_kHz = np.array([704.8, 949.0, 965.2, 1096.3, 1128.4, 1182.8, 1338.9, 1360.9])
computed_freqs_kHz, mode_indices = get_first_N_above_thresh(8, freqs / 1e3, thresh=1, decimals=1)
print('found the following first unique eigenfrequencies:')
for ind, (freq1, freq2) in enumerate(zip(computed_freqs_kHz, expected_freqs_kHz)):
error = np.abs(freq2 - freq1) / freq1 * 100.0
print(f'freq. {ind + 1:1}: {freq1:8.1f} kHz, expected: {freq2:8.1f} kHz, error: {error:.2f} %')
found the following first unique eigenfrequencies:
freq. 1: 705.1 kHz, expected: 704.8 kHz, error: 0.04 %
freq. 2: 949.1 kHz, expected: 949.0 kHz, error: 0.01 %
freq. 3: 965.7 kHz, expected: 965.2 kHz, error: 0.05 %
freq. 4: 1096.3 kHz, expected: 1096.3 kHz, error: 0.00 %
freq. 5: 1128.6 kHz, expected: 1128.4 kHz, error: 0.02 %
freq. 6: 1183.9 kHz, expected: 1182.8 kHz, error: 0.09 %
freq. 7: 1339.0 kHz, expected: 1338.9 kHz, error: 0.01 %
freq. 8: 1361.8 kHz, expected: 1360.9 kHz, error: 0.07 %
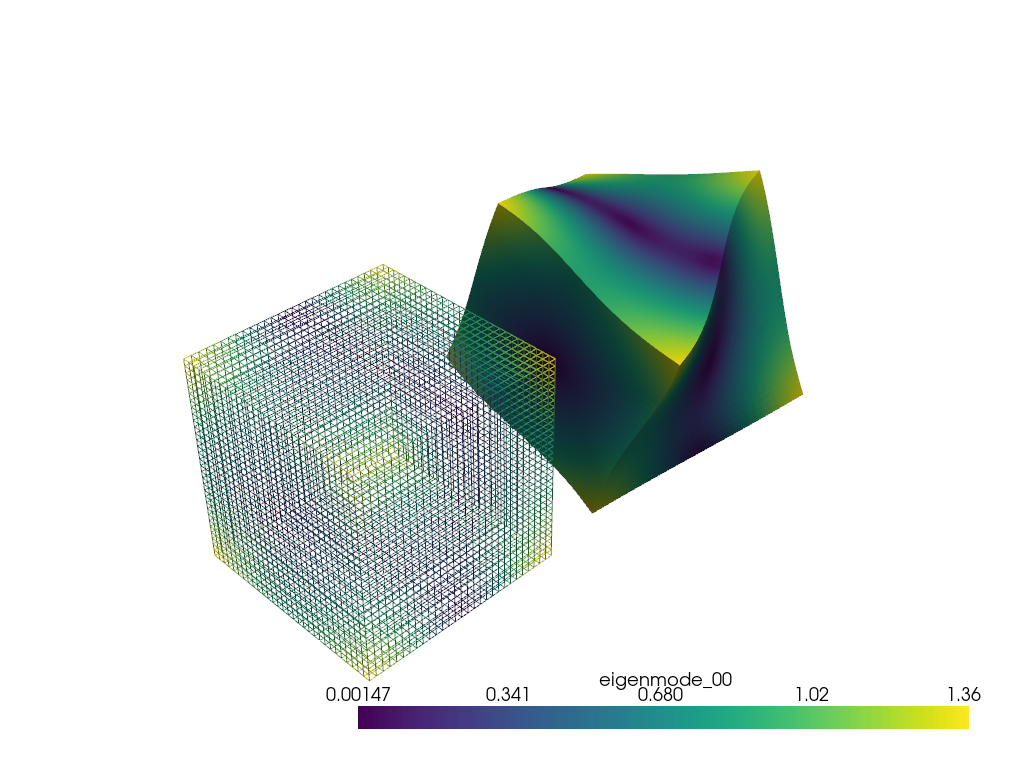
Now, let’s display a mode on a mesh of the cube.
# Create the 3D NumPy array of spatially referenced data
# (nx by ny by nz)
nx, ny, nz = 30, 31, 32
x = np.linspace(-l1 / 2.0, l1 / 2.0, nx)
y = np.linspace(-l2 / 2.0, l2 / 2.0, ny)
x, y = np.meshgrid(x, y)
z = np.zeros_like(x) + l3 / 2.0
grid = pv.StructuredGrid(x, y, z)
slices = []
for zz in np.linspace(-l3 / 2.0, l3 / 2.0, nz)[::-1]:
slice_ = grid.points.copy()
slice_[:, -1] = zz
slices.append(slice_)
vol = pv.StructuredGrid()
vol.points = np.vstack(slices)
vol.dimensions = [*grid.dimensions[0:2], nz]
for i, mode_index in enumerate(mode_indices):
eigenvector = vr[:, mode_index]
displacement_points = np.zeros_like(vol.points)
for weight, (component, p, q, r) in zip(eigenvector, quadruplets):
displacement_points[:, component] += (
weight * vol.points[:, 0] ** p * vol.points[:, 1] ** q * vol.points[:, 2] ** r
)
if displacement_points.max() > 0.0:
displacement_points /= displacement_points.max()
vol[f'eigenmode_{i:02}'] = displacement_points
warpby = 'eigenmode_00'
warped = vol.warp_by_vector(warpby, factor=0.04)
warped.translate([-1.5 * l1, 0.0, 0.0], inplace=True)
pl = pv.Plotter()
pl.add_mesh(vol, style='wireframe', scalars=warpby, show_scalar_bar=False)
pl.add_mesh(warped, scalars=warpby)
pl.show()
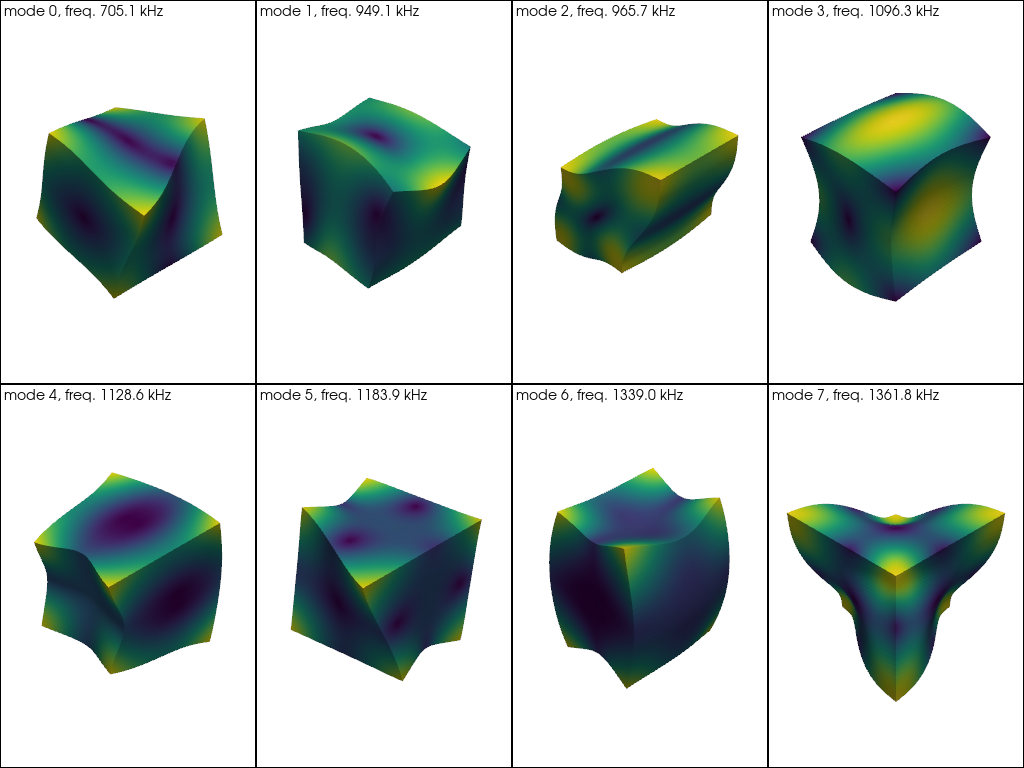
Finally, let’s make a gallery of the first 8 unique eigenmodes.
pl = pv.Plotter(shape=(2, 4))
for i, j in product(range(2), range(4)):
pl.subplot(i, j)
current_index = 4 * i + j
vector = f'eigenmode_{current_index:02}'
pl.add_text(
f'mode {current_index}, freq. {computed_freqs_kHz[current_index]:.1f} kHz',
font_size=10,
)
pl.add_mesh(vol.warp_by_vector(vector, factor=0.03), scalars=vector, show_scalar_bar=False)
pl.show()
Total running time of the script: (0 minutes 6.526 seconds)
