Gaussian Smoothing

Perform a Gaussian convolution on a uniformly gridded data set.

pyvista.ImageData data sets (a.k.a. images) a can be smoothed by convolving the image data set with a Gaussian for one- to three-dimensional inputs. This is commonly referred to as Gaussian blurring and typically used to reduce noise or decrease the detail of an image dataset.

See also pyvista.ImageDataFilters.gaussian_smooth().

from __future__ import annotations

import pyvista as pv
from pyvista import examples

# Load dataset
data = examples.download_gourds()

# Define a good point of view
cp = [(319.5, 239.5, 1053.7372980874645), (319.5, 239.5, 0.0), (0.0, 1.0, 0.0)]

Let’s apply the Gaussian smoothing with different values of standard deviation.

p = pv.Plotter(shape=(2, 2))

p.subplot(0, 0)
p.add_text('Original Image', font_size=14)
p.add_mesh(data, rgb=True)
p.camera_position = cp

p.subplot(0, 1)
p.add_text('Gaussian smoothing, std=2', font_size=14)
p.add_mesh(data.gaussian_smooth(std_dev=2.0), rgb=True)
p.camera_position = cp

p.subplot(1, 0)
p.add_text('Gaussian smoothing, std=4', font_size=14)
p.add_mesh(data.gaussian_smooth(std_dev=4.0), rgb=True)
p.camera_position = cp

p.subplot(1, 1)
p.add_text('Gaussian smoothing, std=8', font_size=14)
p.add_mesh(data.gaussian_smooth(std_dev=8.0), rgb=True)
p.camera_position = cp

p.show()

Static Scene

Interactive Scene

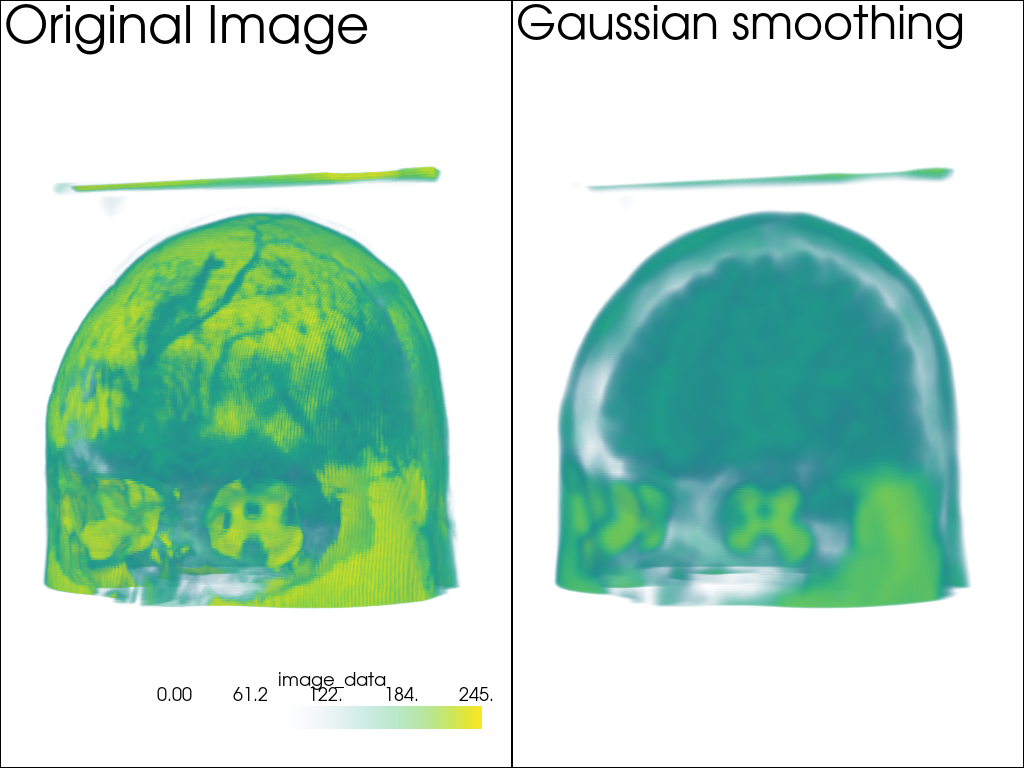
Volume Rendering

Now let’s see an example on a 3D dataset with volume rendering:

data = examples.download_brain()

smoothed_data = data.gaussian_smooth(std_dev=3.0)


dargs = dict(clim=smoothed_data.get_data_range(), opacity=[0, 0, 0, 0.1, 0.3, 0.6, 1])

n = [100, 150, 200, 245, 255]

p = pv.Plotter(shape=(1, 2))
p.subplot(0, 0)
p.add_text('Original Image', font_size=24)
# p.add_mesh(data.contour(n), **dargs)
p.add_volume(data, **dargs)
p.subplot(0, 1)
p.add_text('Gaussian smoothing', font_size=24)
# p.add_mesh(smoothed_data.contour(n), **dargs)
p.add_volume(smoothed_data, **dargs)
p.link_views()
p.camera_position = [(-162.0, 704.8, 65.02), (90.0, 108.0, 90.0), (0.0068, 0.0447, 0.999)]
p.show()

Tags: filter