Unstructured Grid with Polyhedra

This example shows how to build a simple pyvista.UnstructuredGrid using polyhedra. We will be using VTK types to determine which type of cells we are building.

First, we import the required libraries.

import pyvista as pv

Define Points

We will mix several cells in one grid for this example. Here we create the points that will define each cell.

Note

It is not necessary that each cell has an isolated set of points. This has been done here to create isolated cells for this example.

quad_points = [
    [0.0, 0.0, 0.0],  # 0
    [0.0, 0.01, 0.0],  # 1
    [0.01, 0.01, 0.0],  # 2
    [0.01, 0.0, 0.0],  # 3
]
polygon_points = [
    [0.02, 0.0, 0.0],  # 4
    [0.02, 0.01, 0.0],  # 5
    [0.03, 0.01, 0.0],  # 6
    [0.035, 0.005, 0.0],  # 7
    [0.03, 0.0, 0.0],  # 8
]
hexa_points = [
    [0.0, 0.0, 0.02],  # 9
    [0.0, 0.01, 0.02],  # 10
    [0.01, 0.01, 0.02],  # 11
    [0.01, 0.0, 0.02],  # 12
    [0.0, 0.0, 0.03],  # 13
    [0.0, 0.01, 0.03],  # 14
    [0.01, 0.01, 0.03],  # 15
    [0.01, 0.0, 0.03],  # 16
]
polyhedron_points = [
    [0.02, 0.0, 0.02],  # 17
    [0.02, 0.01, 0.02],  # 18
    [0.03, 0.01, 0.02],  # 19
    [0.035, 0.005, 0.02],  # 20
    [0.03, 0.0, 0.02],  # 21
    [0.02, 0.0, 0.03],  # 22
    [0.02, 0.01, 0.03],  # 23
    [0.03, 0.01, 0.03],  # 24
    [0.035, 0.005, 0.03],  # 25
    [0.03, 0.0, 0.03],  # 26
]
points = quad_points + polygon_points + hexa_points + polyhedron_points

Cell connectivity

Connectivity describes the indices of the points to compose each cell. The first item in each cell’s connectivity is the number of items the cell will have. For example, a quad cell is composed of points [0, 1, 2, 3] and totaling 4 points, therefore [4, 0, 1, 2, 3] describes its connectivity.

Note

This example uses lists for simplicity, but internally PyVista converts these lists to a numpy.ndarray with dtype=pyvista.ID_TYPE and passes it to VTK.

The same approach can be applied to all the other cell types.

quad = [4, 0, 1, 2, 3]
polygon = [5, 4, 5, 6, 7, 8]
hexa = [8, 9, 10, 11, 12, 13, 14, 15, 16]

Polyhedron connectivity array

The connectivity array of polyhedra is defined differently from the rest of the cell types. For polyhedra, we need to set the faces with the following format:

[NItems, NFaces, Face0NPoints, Face0Point0, Face0Point1..., Face0PointN-1, Face1NPoints, ...]

Where:

• NItems refers to the total number of items in the list needed to describe the polyhedron.

• NFaces is the number of faces the polyhedron will have.

• Face0NPoints is the number of points the first face will have.

• Face0Point0...Face0PointN-1 are each of the points that describe face0.

In polyhedron_connectivity, the first item is NFaces. NItems is added to polyhedron.

polyhedron_connectivity = [
    # NItems will go here
    7,  # number of faces
    5,  # number of points in face0
    17,  # point index 0
    18,  # point index 1
    19,  # point index 2
    20,  # point index 3
    21,  # point index 4
    4,  # number of points in face1
    17,  # point index ...
    18,
    23,
    22,
    4,
    17,
    21,
    26,
    22,
    4,
    21,
    26,
    25,
    20,
    4,
    20,
    25,
    24,
    19,
    4,
    19,
    24,
    23,
    18,
    5,
    22,
    23,
    24,
    25,
    26,
]

# note how we retroactively add NItems
polyhedron = [len(polyhedron_connectivity)] + polyhedron_connectivity

Cells array

Now we build the input cells array for the pyvista.UnstructuredGrid. Here, we join all cells in a flat list. Internally, the NItems previously described is used to determine which nodes belong to which cells.

cells = quad + polygon + hexa + polyhedron

Cell types

We need to specify the cell types for each of the cells we define in the cells array.

The number of items in this list must match the number of cells in the connectivity array.

celltypes = [pv.CellType.QUAD, pv.CellType.POLYGON, pv.CellType.HEXAHEDRON, pv.CellType.POLYHEDRON]

Create the grid

To create the grid, we use the cells array we built, the cell types, and the points that describe the faces.

grid = pv.UnstructuredGrid(cells, celltypes, points)

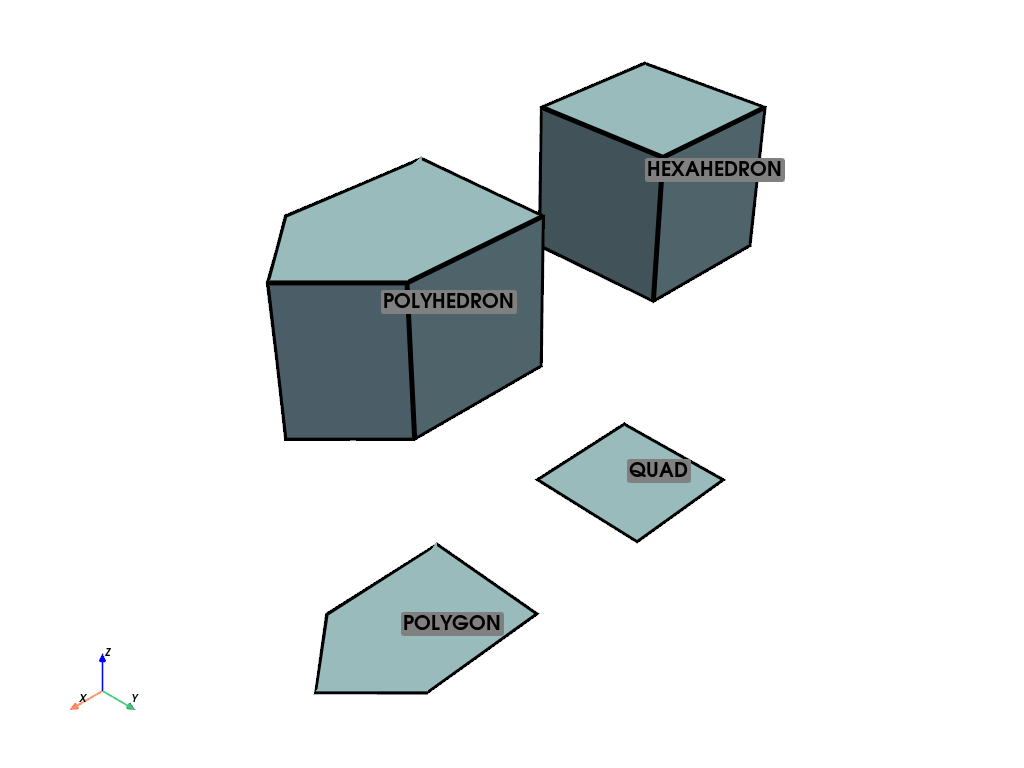
Plot the mesh

Finally, we can plot the grid we’ve created. Label each cell at its cell center for clarity.

pl = pv.Plotter()
pl.show_axes()
pl.add_mesh(grid, show_edges=True, line_width=5)
pl.add_point_labels(
    grid.cell_centers().points,
    ['QUAD', 'POLYGON', 'HEXAHEDRON', 'POLYHEDRON'],
    always_visible=True,
    font_size=20,
)
pl.show()