Distance Between Two Surfaces

Compute the average thickness between two surfaces.

For example, you might have two surfaces that represent the boundaries of lithological layers in a subsurface geological model and you want to know the average thickness of a unit between those boundaries.

A clarification on terminology in this example is important. A mesh point exists on the vertex of each cell on the mesh. See What is a Mesh?. Each cell in this example encompasses a 2D region of space which contains an infinite number of spatial points; these spatial points are not mesh points. The distance between two surfaces can mean different things depending on context and usage. Each example here explores different aspects of the distance from the vertex points of the bottom mesh to the top mesh.

First, we will demo a method where we compute the normals on the vertex points of the bottom surface, and then project a ray to the top surface to compute the distance along the surface normals. This ray will usually intersect the top surface at a spatial point inside a cell of the mesh.

Second, we will use a KDTree to compute the distance from every vertex point in the bottom mesh to its closest vertex point in the top mesh.

Lastly, we will use a PyVista filter, pyvista.DataSet.find_closest_cell() to calculate the distance from every vertex point in the bottom mesh to the closest spatial point inside a cell of the top mesh. This will be the shortest distance from the vertex point to the top surface, unlike the first two examples.

from __future__ import annotations

import numpy as np

import pyvista as pv


def hill(seed):
    """Make a random surface."""
    mesh = pv.ParametricRandomHills(random_seed=seed, u_res=50, v_res=50, hill_amplitude=0.5)
    mesh.rotate_y(-10, inplace=True)  # give the surfaces some tilt

    return mesh


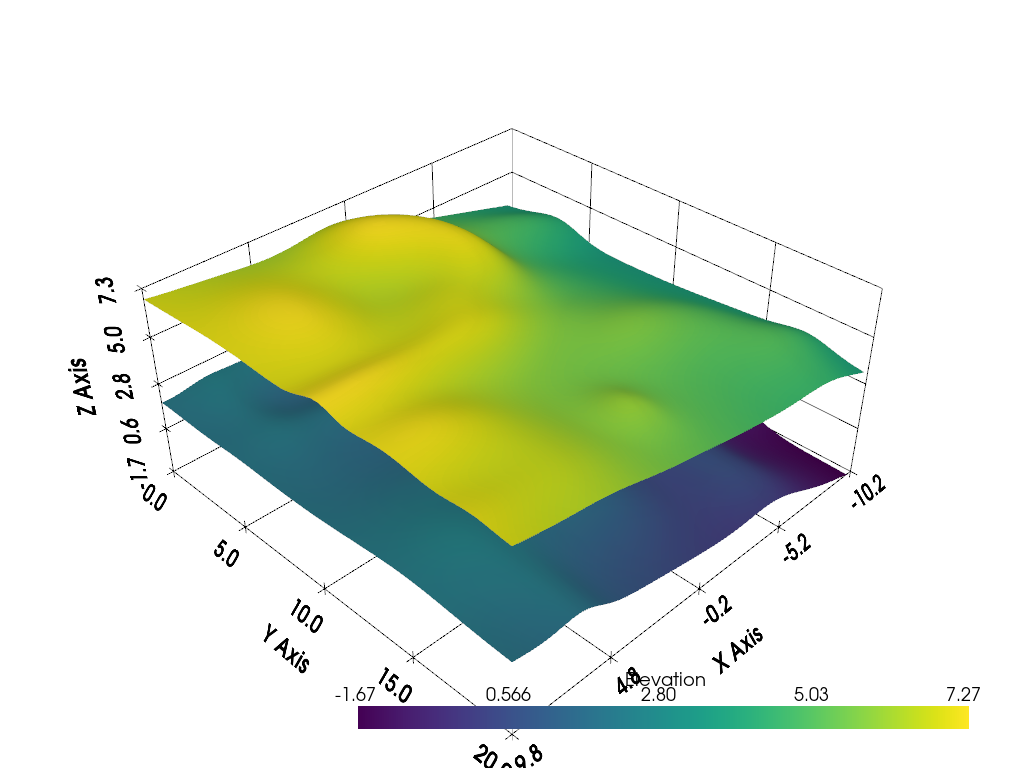
h0 = hill(1).elevation()
h1 = hill(10)
# Shift one surface
h1.points[:, -1] += 5
h1 = h1.elevation()

p = pv.Plotter()
p.add_mesh(h0, smooth_shading=True)
p.add_mesh(h1, smooth_shading=True)
p.show_grid()
p.show()

Static Scene

Interactive Scene

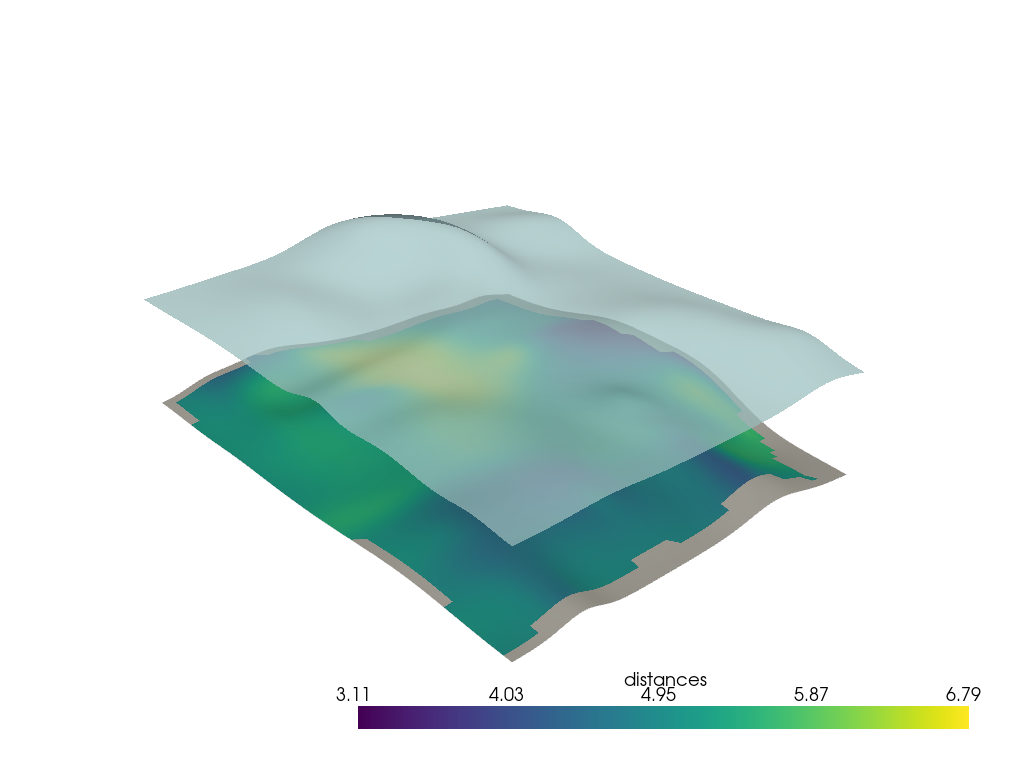
Ray Tracing Distance

Compute normals of lower surface at vertex points

h0n = h0.compute_normals(point_normals=True, cell_normals=False, auto_orient_normals=True)

Travel along normals to the other surface and compute the thickness on each vector.

h0n['distances'] = np.empty(h0.n_points)
for i in range(h0n.n_points):
    p = h0n.points[i]
    vec = h0n['Normals'][i] * h0n.length
    p0 = p - vec
    p1 = p + vec
    ip, ic = h1.ray_trace(p0, p1, first_point=True)
    dist = np.sqrt(np.sum((ip - p) ** 2))
    h0n['distances'][i] = dist

# Replace zeros with nans
mask = h0n['distances'] == 0
h0n['distances'][mask] = np.nan
np.nanmean(h0n['distances'])

np.float64(5.144072856644497)

p = pv.Plotter()
p.add_mesh(h0n, scalars='distances', smooth_shading=True)
p.add_mesh(h1, color=True, opacity=0.75, smooth_shading=True)
p.show()

Static Scene

Interactive Scene

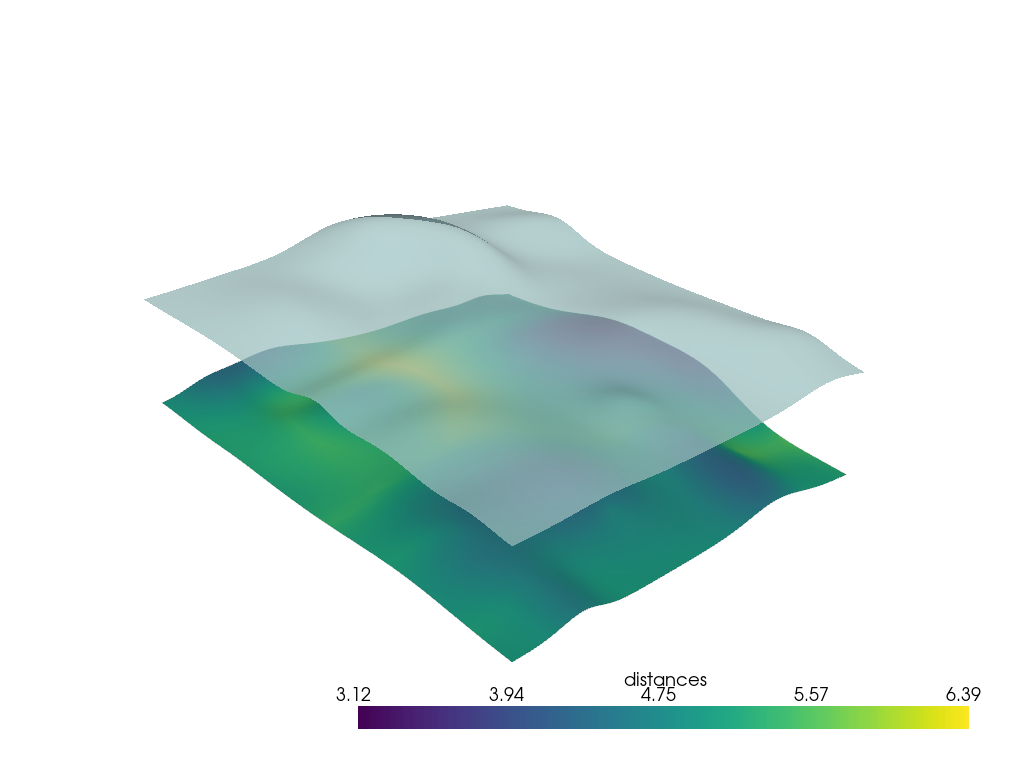
Nearest Neighbor Distance

You could also use a KDTree to compare the distance between each vertex point of the upper surface and the nearest neighbor vertex point of the lower surface. This will be noticeably faster than a ray trace, especially for large surfaces.

from scipy.spatial import KDTree

tree = KDTree(h1.points)
d_kdtree, idx = tree.query(h0.points)
h0['distances'] = d_kdtree
np.mean(d_kdtree)

np.float64(4.843639418894909)

p = pv.Plotter()
p.add_mesh(h0, scalars='distances', smooth_shading=True)
p.add_mesh(h1, color=True, opacity=0.75, smooth_shading=True)
p.show()

Static Scene

Interactive Scene

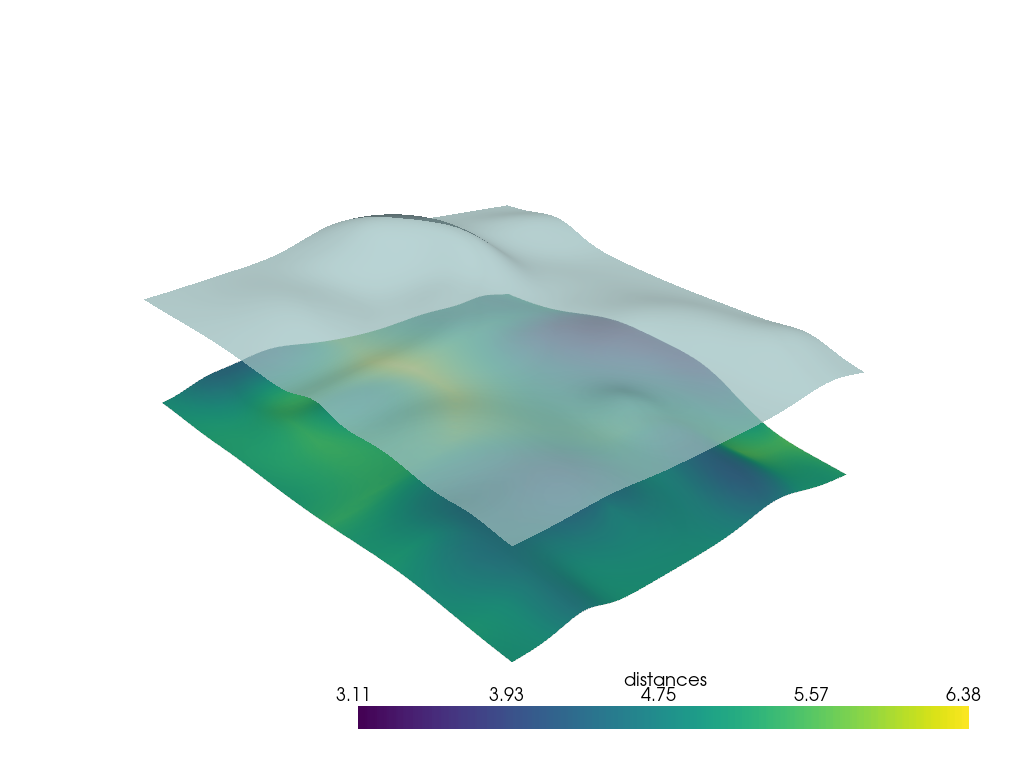
Using PyVista Filter

The pyvista.DataSet.find_closest_cell() filter returns the spatial points inside the cells of the top surface that are closest to the vertex points of the bottom surface. closest_points is returned when using return_closest_point=True.

closest_cells, closest_points = h1.find_closest_cell(h0.points, return_closest_point=True)
d_exact = np.linalg.norm(h0.points - closest_points, axis=1)
h0['distances'] = d_exact
np.mean(d_exact)

np.float64(4.841284523106411)

As expected there is only a small difference between this method and the KDTree method.

p = pv.Plotter()
p.add_mesh(h0, scalars='distances', smooth_shading=True)
p.add_mesh(h1, color=True, opacity=0.75, smooth_shading=True)
p.show()

Static Scene

Interactive Scene

Tags: filter