Boolean Operations

Perform boolean operations with closed (manifold) surfaces.

Boolean/topological operations (intersect, union, difference) methods are implemented for pyvista.PolyData mesh types only and are accessible directly from any pyvista.PolyData mesh. Check out pyvista.PolyDataFilters and take a look at the following filters:

• pyvista.PolyDataFilters.boolean_difference()

• pyvista.PolyDataFilters.boolean_union()

• pyvista.PolyDataFilters.boolean_intersection()

Essentially, boolean union, difference, and intersection are all the same operation. Just different parts of the objects are kept at the end.

The - operator can be used between any two pyvista.PolyData meshes in PyVista to cut the first mesh by the second. These meshes must be all triangle meshes, which you can check with pyvista.PolyData.is_all_triangles.

Note

For merging, the + operator can be used between any two meshes in PyVista which simply calls the .merge() filter to combine any two meshes. This is different from the operator | in PyVista which simply calls the boolean_union filter as it simply superimposes the two meshes without performing additional calculations on the result. The & operator in PyVista simply calls the boolean_intersection.

Warning

If your boolean operations don’t react the way you think they should (i.e. the wrong parts disappear), one of your meshes probably has its normals pointing inward. Use pyvista.PolyDataFilters.plot_normals() to visualize the normals.

from __future__ import annotations

import pyvista as pv

sphere_a = pv.Sphere()
sphere_b = pv.Sphere(center=(0.5, 0, 0))

Boolean Union

Perform a boolean union of A and B using the pyvista.PolyDataFilters.boolean_union() filter.

The union of two manifold meshes A and B is the mesh which is in A, in B, or in both A and B.

Order of operands does not matter for boolean union (the operation is commutative).

result = sphere_a | sphere_b
pl = pv.Plotter()
_ = pl.add_mesh(sphere_a, color='r', style='wireframe', line_width=3)
_ = pl.add_mesh(sphere_b, color='b', style='wireframe', line_width=3)
_ = pl.add_mesh(result, color='lightblue')
pl.camera_position = 'xz'
pl.show()

Static Scene

Interactive Scene

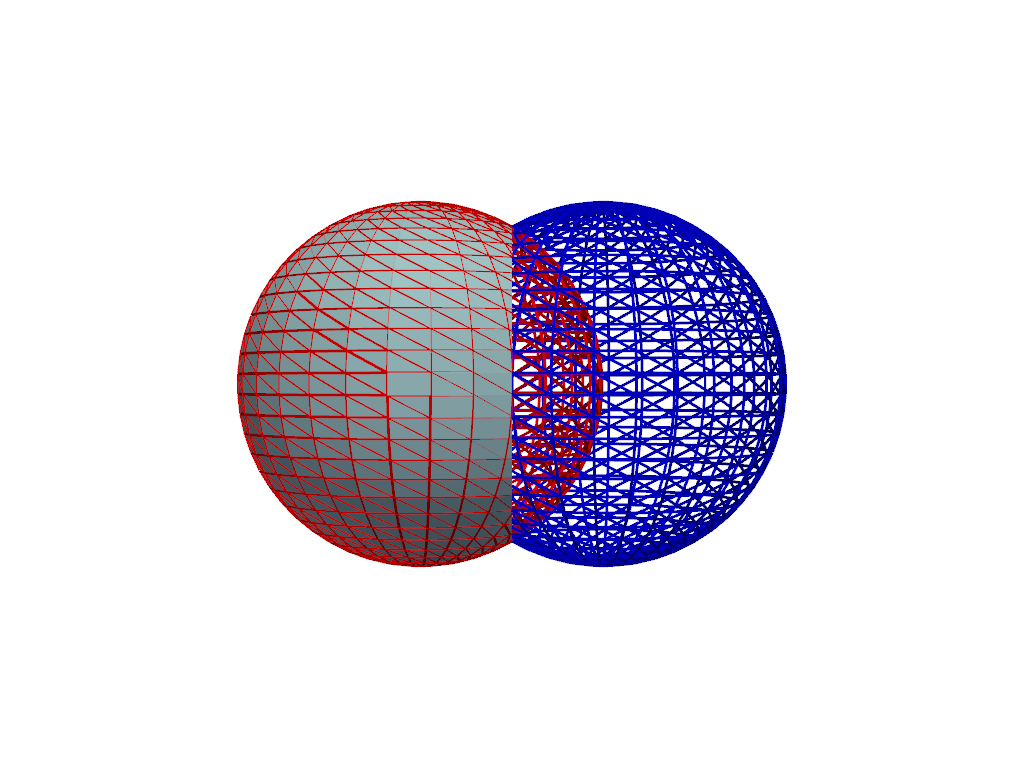
Boolean Difference

Perform a boolean difference of A and B using the pyvista.PolyDataFilters.boolean_difference() filter or the - operator since both meshes are pyvista.PolyData.

The difference of two manifold meshes A and B is the volume of the mesh in A not belonging to B.

Order of operands matters for boolean difference.

result = sphere_a - sphere_b
pl = pv.Plotter()
_ = pl.add_mesh(sphere_a, color='r', style='wireframe', line_width=3)
_ = pl.add_mesh(sphere_b, color='b', style='wireframe', line_width=3)
_ = pl.add_mesh(result, color='lightblue')
pl.camera_position = 'xz'
pl.show()

Static Scene

Interactive Scene

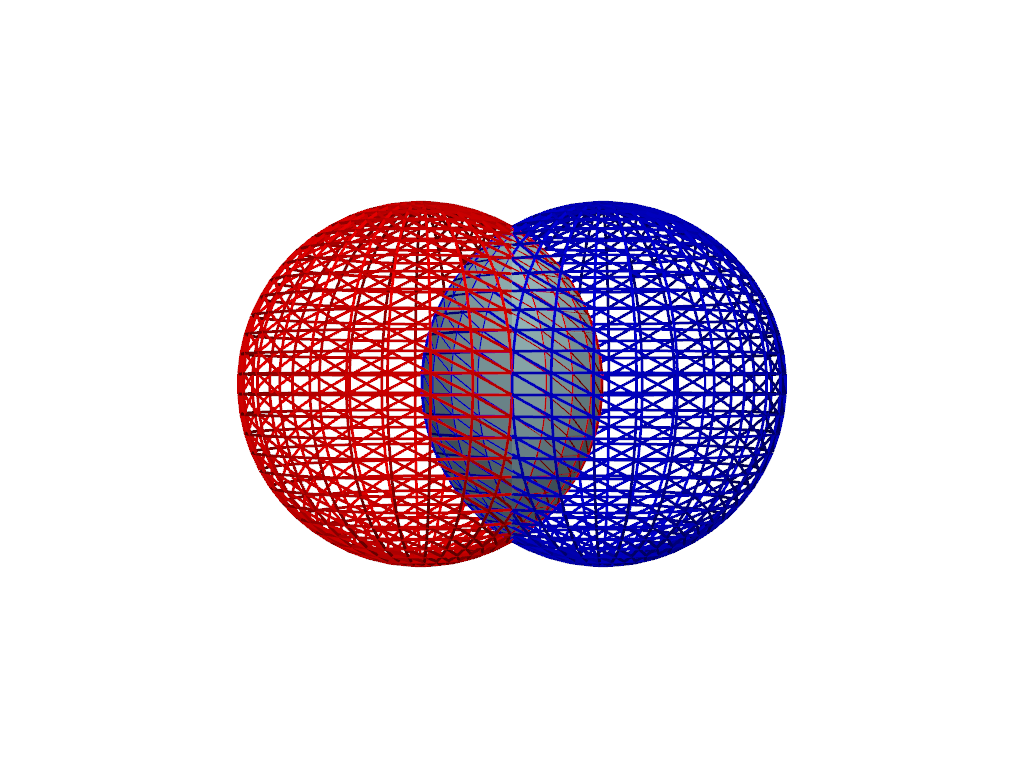
Boolean Intersection

Perform a boolean intersection of A and B using the pyvista.PolyDataFilters.boolean_intersection() filter.

The intersection of two manifold meshes A and B is the mesh which is the volume of A that is also in B.

Order of operands does not matter for boolean intersection (the operation is commutative).

result = sphere_a & sphere_b
pl = pv.Plotter()
_ = pl.add_mesh(sphere_a, color='r', style='wireframe', line_width=3)
_ = pl.add_mesh(sphere_b, color='b', style='wireframe', line_width=3)
_ = pl.add_mesh(result, color='lightblue')
pl.camera_position = 'xz'
pl.show()

Static Scene

Interactive Scene

Behavior due to flipped normals

Note that these boolean filters behave differently depending on the orientation of the normals.

Boolean difference with both cube and sphere normals pointed outward. This is the “normal” behavior.

cube = pv.Cube().triangulate().subdivide(3)
sphere = pv.Sphere(radius=0.6)
result = cube.boolean_difference(sphere)
result.plot(color='lightblue')

Static Scene

Interactive Scene

Boolean difference with cube normals outward, sphere inward.

cube = pv.Cube().triangulate().subdivide(3)
sphere = pv.Sphere(radius=0.6)
sphere.flip_normals()
result = cube.boolean_difference(sphere)
result.plot(color='lightblue')

Static Scene

Interactive Scene

Boolean difference with cube normals inward, sphere outward.

cube = pv.Cube().triangulate().subdivide(3)
cube.flip_normals()
sphere = pv.Sphere(radius=0.6)
result = cube.boolean_difference(sphere)
result.plot(color='lightblue')

Static Scene

Interactive Scene

Both cube and sphere normals inward.

cube = pv.Cube().triangulate().subdivide(3)
cube.flip_normals()
sphere = pv.Sphere(radius=0.6)
sphere.flip_normals()
result = cube.boolean_difference(sphere)
result.plot(color='lightblue')

Static Scene

Interactive Scene

Tags: filter