Terrain Following Mesh

Use a topographic surface to create a 3D terrain-following mesh.

Terrain following meshes are common in the environmental sciences, for instance in hydrological modelling (see Maxwell 2013 and ParFlow).

In this example, we demonstrate a simple way to make a 3D grid/mesh that follows a given topographic surface. In this example, it is important to note that the given digital elevation model (DEM) is structured (gridded and not triangulated): this is common for DEMs.

from __future__ import annotations

import numpy as np

import pyvista as pv
from pyvista import examples

Download a gridded topography surface (DEM)

dem = examples.download_crater_topo()
dem

Header	Data Arrays
ImageData Information N Cells 1677401 N Points 1680000 X Bounds 1.810e+06, 1.831e+06 Y Bounds 5.640e+06, 5.658e+06 Z Bounds 0.000e+00, 0.000e+00 Dimensions 1400, 1200, 1 Spacing 1.500e+01, 1.500e+01, 0.000e+00 N Arrays 1	Name Field Type N Comp Min Max scalar1of1 Points float64 1 7.339e+02 2.787e+03

Now let’s subsample and extract an area of interest to make this example simple (also the DEM we just load is pretty big). Since the DEM we loaded is a pyvista.ImageData mesh, we can use the pyvista.ImageDataFilters.extract_subset() filter:

subset = dem.extract_subset((500, 900, 400, 800, 0, 0), (5, 5, 1))
subset.plot(cpos='xy')

Static Scene

Interactive Scene

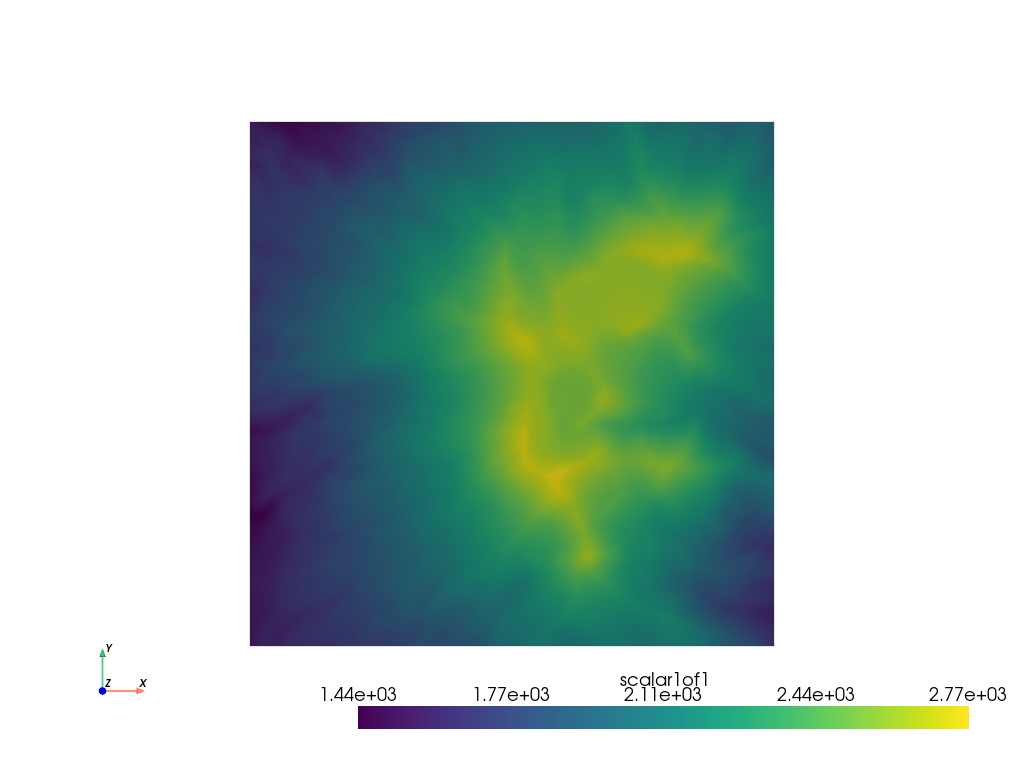
Now that we have a region of interest for our terrain following mesh, lets make a 3D surface of that DEM:

terrain = subset.warp_by_scalar()
terrain

Header	Data Arrays
StructuredGrid Information N Cells 6400 N Points 6561 X Bounds 1.818e+06, 1.824e+06 Y Bounds 5.646e+06, 5.652e+06 Z Bounds 1.441e+03, 2.769e+03 Dimensions 81, 81, 1 N Arrays 1	Name Field Type N Comp Min Max scalar1of1 Points float64 1 1.441e+03 2.769e+03

terrain.plot()

Static Scene

Interactive Scene

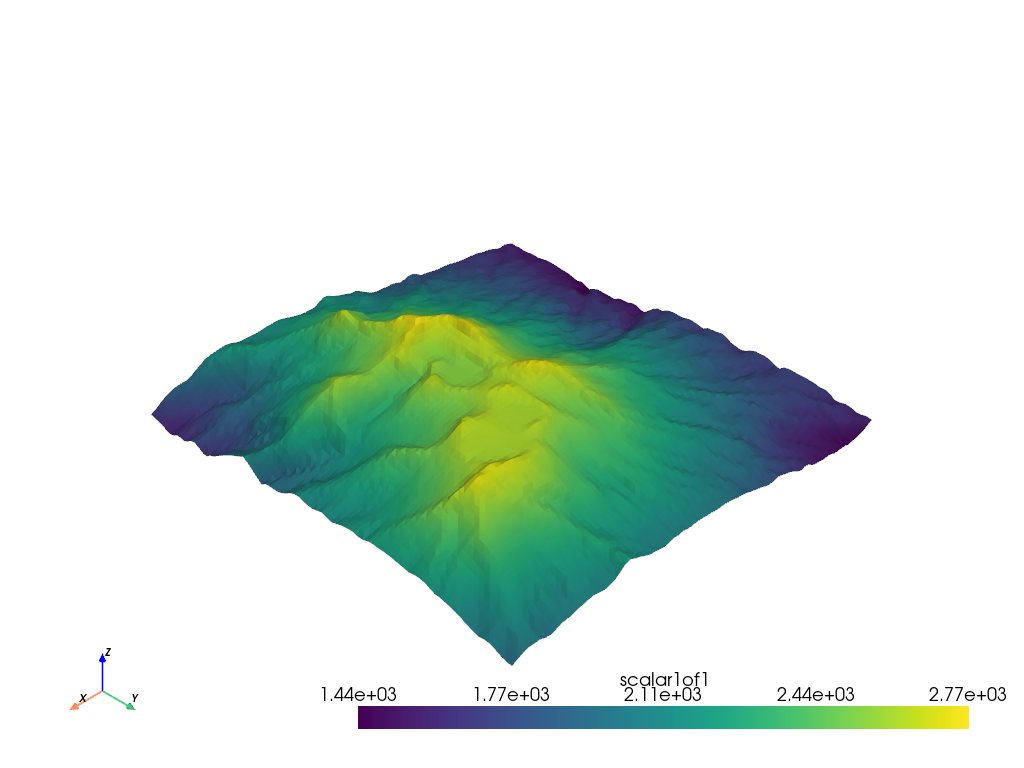
And now we have a 3D structured surface of the terrain. We can now extend that structured surface into a 3D mesh to form a terrain following grid. To do this, we first our cell spacings in the z-direction (these start from the terrain surface). Then we repeat the XYZ structured coordinates of the terrain mesh and decrease each Z level by our Z cell spacing. Once we have those structured coordinates, we can create a pyvista.StructuredGrid.

z_cells = np.array([25] * 5 + [35] * 3 + [50] * 2 + [75, 100])

xx = np.repeat(terrain.x, len(z_cells), axis=-1)
yy = np.repeat(terrain.y, len(z_cells), axis=-1)
zz = np.repeat(terrain.z, len(z_cells), axis=-1) - np.cumsum(z_cells).reshape((1, 1, -1))

mesh = pv.StructuredGrid(xx, yy, zz)
mesh['Elevation'] = zz.ravel(order='F')
mesh

Header	Data Arrays
StructuredGrid Information N Cells 70400 N Points 78732 X Bounds 1.818e+06, 1.824e+06 Y Bounds 5.646e+06, 5.652e+06 Z Bounds 9.364e+02, 2.744e+03 Dimensions 81, 81, 12 N Arrays 1	Name Field Type N Comp Min Max Elevation Points float64 1 9.364e+02 2.744e+03

cpos = [
    (1826736.796308761, 5655837.275274233, 4676.8405505181745),
    (1821066.1790519988, 5649248.765538796, 943.0995128226014),
    (-0.2797856225380979, -0.27966946337594883, 0.9184252809434081),
]

mesh.plot(show_edges=True, lighting=False, cpos=cpos)

Static Scene

Interactive Scene

Tags: load