pyvista.Icosphere

Icosphere(

radius: float = 1.0,

center: VectorLike[float] = (0.0, 0.0, 0.0),

nsub: int = 3,

) → PolyData

Create an icosphere.

An icosphere is a geodesic polyhedron, which is a convex polyhedron made from triangles.

Geodesic polyhedra are constructed by subdividing faces of simpler polyhedra, and then projecting the new vertices onto the surface of a sphere. A geodesic polyhedron has straight edges and flat faces that approximate a sphere,

Parameters:

radiusfloat, default: 1.0

Radius of the icosphere.

centersequence[float], default: (0.0, 0.0, 0.0)

Center of the icosphere.

nsubint, default: 3

This is the number of times each triangle of the original pyvista.Icosahedron() is subdivided.

Returns:

pyvista.PolyData

Mesh of the icosphere.

See also

pyvista.Sphere

Examples

Create the icosphere and plot it with edges.

>>> import pyvista as pv
>>> icosphere = pv.Icosphere()
>>> icosphere.plot(show_edges=True)

Static Scene

Interactive Scene

Show how this icosphere was created.

>>> import numpy as np
>>> icosahedron = pv.Icosahedron()
>>> icosahedron.clear_data()  # remove extra scalars
>>> icosahedron_sub = icosahedron.subdivide(nsub=3)
>>> pl = pv.Plotter(shape=(1, 3))
>>> _ = pl.add_mesh(icosahedron, show_edges=True)
>>> pl.subplot(0, 1)
>>> _ = pl.add_mesh(icosahedron_sub, show_edges=True)
>>> pl.subplot(0, 2)
>>> _ = pl.add_mesh(icosphere, show_edges=True)
>>> pl.show()

Static Scene

Interactive Scene

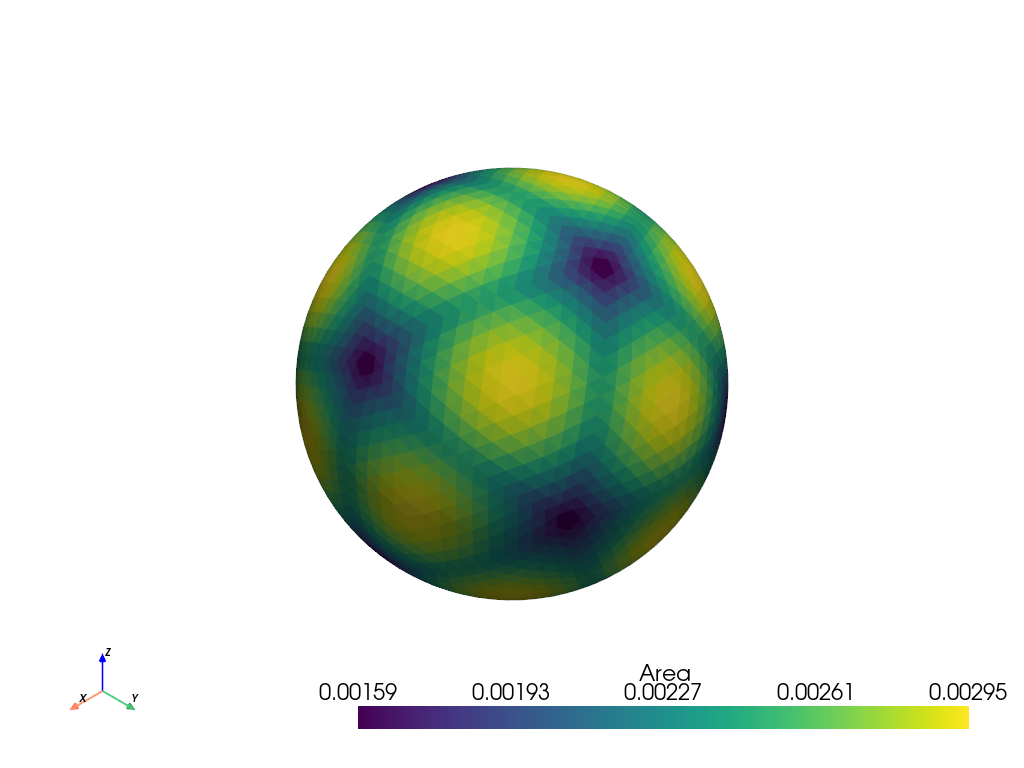
Show how the triangles are not uniform in area. This is because the ones farther from the edges from the original triangles have farther to travel to the sphere.

>>> icosphere = pv.Icosphere(nsub=4)
>>> icosphere.compute_cell_sizes().plot(scalars='Area')

Static Scene

Interactive Scene