pyvista.Transform#
- class Transform(*args, **kwargs)[source]#
Describes linear transformations via a 4x4 matrix.
A
Transformcan be used to describe the full range of linear (also known as affine) coordinate transformations in three dimensions, which are internally represented as a 4x4 homogeneous transformation matrix.The transformation methods (e.g.
translate(),rotate(),compose()) can operate in eitherpre_multiply()orpost_multiply()mode. In pre-multiply mode, any additional transformations will occur before any transformations represented by the currentmatrix. In post-multiply mode (the default), the additional transformation will occur after any transformations represented by the current matrix.Note
This class performs all of its operations in a right-handed coordinate system with right-handed rotations. Some other graphics libraries use left-handed coordinate systems and rotations.
Added in version 0.45.
- Parameters:
- trans
TransformLike|Sequence[TransformLike],optional Initialize the transform with a transformation or sequence of transformations. By default, the transform is initialized as the identity matrix.
- point
VectorLike[float],optional Point to use when composing transformations. If set, two additional transformations are composed and added to the
matrix_list:translate()topointbefore the transformationtranslate()away frompointafter the transformation
By default, this value is
None, which means that the scale, rotation, etc. transformations are performed about the origin(0, 0, 0).- multiply_mode‘pre’ | ‘post’,
optional Multiplication mode to use when composing. Set this to
'pre'for pre-multiplication or'post'for post-multiplication.
- trans
See also
pyvista.DataObjectFilters.transformApply a transformation to a mesh.
pyvista.Prop3D.transformTransform an actor.
Examples
Create a transformation and use
+to compose a translation.>>> import numpy as np >>> import pyvista as pv >>> position = (-0.6, -0.8, 2.1) >>> translation_T = pv.Transform() + position >>> translation_T.matrix array([[ 1. , 0. , 0. , -0.6], [ 0. , 1. , 0. , -0.8], [ 0. , 0. , 1. , 2.1], [ 0. , 0. , 0. , 1. ]])
Using
+performs the same concatenation as callingtranslate().>>> np.array_equal( ... translation_T.matrix, pv.Transform().translate(position).matrix ... ) True
Create a transformation and use
*to compose a scaling matrix.>>> scale_factor = 2.0 >>> scaling_T = pv.Transform() * scale_factor >>> scaling_T.matrix array([[2., 0., 0., 0.], [0., 2., 0., 0.], [0., 0., 2., 0.], [0., 0., 0., 1.]])
Using
*performs the same concatenation as callingscale().>>> np.array_equal(scaling_T.matrix, pv.Transform().scale(scale_factor).matrix) True
Compose the two transformations using
*. This will compose with post-multiplication such that the transformations are applied in order from left to right, i.e. translate first, then scale.>>> transform_post = translation_T * scaling_T >>> transform_post.matrix array([[ 2. , 0. , 0. , -1.2], [ 0. , 2. , 0. , -1.6], [ 0. , 0. , 2. , 4.2], [ 0. , 0. , 0. , 1. ]])
Post-multiplication is equivalent to using matrix multiplication on the arrays directly but with the arguments reversed:
>>> mat_mul = scaling_T.matrix @ translation_T.matrix >>> np.array_equal(transform_post.matrix, mat_mul) True
Alternatively, compose the transformations by chaining the methods with a single
Transforminstance. Note that post-multiply is used by default.>>> transform_post = pv.Transform() >>> transform_post.multiply_mode 'post' >>> _ = transform_post.translate(position).scale(scale_factor) >>> transform_post.matrix array([[ 2. , 0. , 0. , -1.2], [ 0. , 2. , 0. , -1.6], [ 0. , 0. , 2. , 4.2], [ 0. , 0. , 0. , 1. ]])
Use
n_transformationsto check that there are two transformations.>>> transform_post.n_transformations 2
Use
matrix_listto get a list of the transformations. Since post-multiplication is used, the translation matrix is first in the list since it was applied first, and the scale matrix is second.>>> transform_post.matrix_list[0] # translation array([[ 1. , 0. , 0. , -0.6], [ 0. , 1. , 0. , -0.8], [ 0. , 0. , 1. , 2.1], [ 0. , 0. , 0. , 1. ]])
>>> transform_post.matrix_list[1] # scaling array([[2., 0., 0., 0.], [0., 2., 0., 0.], [0., 0., 2., 0.], [0., 0., 0., 1.]])
Create a similar transform but use pre-multiplication this time. Compose the transformations in the same order as before using
translate()andscale().>>> transform_pre = pv.Transform().pre_multiply() >>> _ = transform_pre.translate(position).scale(scale_factor)
This is equivalent to using matrix multiplication directly on the arrays:
>>> mat_mul = translation_T.matrix @ scaling_T.matrix >>> np.array_equal(transform_pre.matrix, mat_mul) True
Show the matrix list again. Note how the order with pre-multiplication is the reverse of post-multiplication.
>>> transform_pre.matrix_list[0] # scaling array([[2., 0., 0., 0.], [0., 2., 0., 0.], [0., 0., 2., 0.], [0., 0., 0., 1.]])
>>> transform_pre.matrix_list[1] # translation array([[ 1. , 0. , 0. , -0.6], [ 0. , 1. , 0. , -0.8], [ 0. , 0. , 1. , 2.1], [ 0. , 0. , 0. , 1. ]])
Apply the two post- and pre-multiplied transformations to a dataset and plot them. Note how the meshes have different positions since post- and pre-multiplication produce different transformations.
>>> mesh_post = pv.Sphere().transform(transform_post, inplace=False) >>> mesh_pre = pv.Cone().transform(transform_pre, inplace=False) >>> pl = pv.Plotter() >>> _ = pl.add_mesh(mesh_post, color='goldenrod') >>> _ = pl.add_mesh(mesh_pre, color='teal') >>> _ = pl.add_axes_at_origin() >>> pl.show()
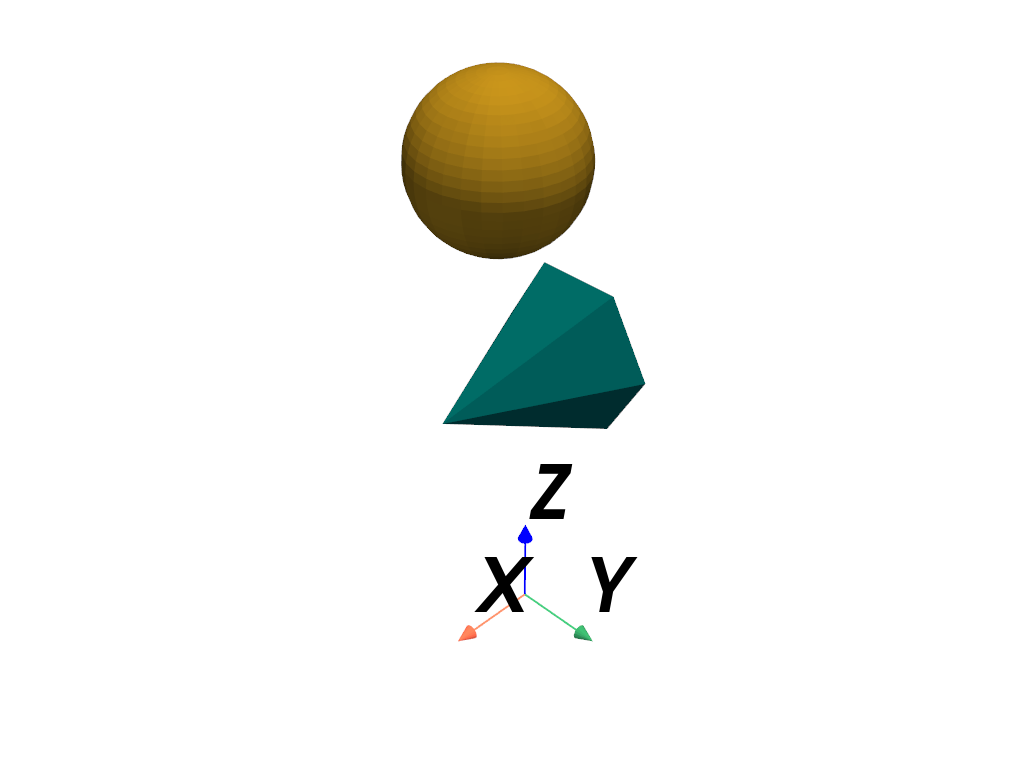
Get the composed inverse transformation matrix of the pre-multiplication case.
>>> inverse_matrix = transform_pre.inverse_matrix >>> inverse_matrix array([[ 0.5 , 0. , 0. , 0.3 ], [ 0. , 0.5 , 0. , 0.4 ], [ 0. , 0. , 0.5 , -1.05], [ 0. , 0. , 0. , 1. ]])
Similar to using
matrix_list, we can inspect the individual transformation inverses withinverse_matrix_list.>>> transform_pre.inverse_matrix_list[0] # inverse scaling array([[0.5, 0. , 0. , 0. ], [0. , 0.5, 0. , 0. ], [0. , 0. , 0.5, 0. ], [0. , 0. , 0. , 1. ]])
>>> transform_pre.inverse_matrix_list[1] # inverse translation array([[ 1. , 0. , 0. , 0.6], [ 0. , 1. , 0. , 0.8], [ 0. , 0. , 1. , -2.1], [ 0. , 0. , 0. , 1. ]])
Transform the mesh by its inverse to restore it to its original un-scaled state and positioning at the origin.
>>> mesh_pre_inverted = mesh_pre.transform(inverse_matrix, inplace=False) >>> pl = pv.Plotter() >>> _ = pl.add_mesh(mesh_pre_inverted, color='teal') >>> _ = pl.add_axes_at_origin() >>> pl.show()
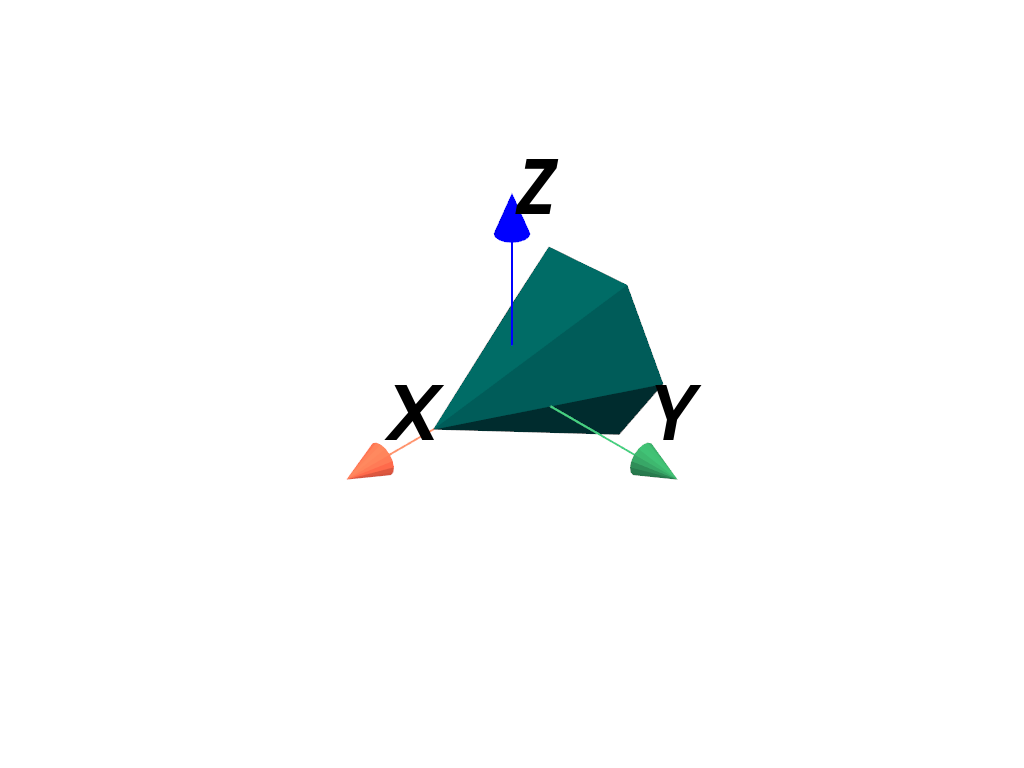
Methods#
|
Apply the current transformation |
|
Apply the current transformation |
|
Apply the current transformation |
|
Apply the current transformation |
|
Apply the current transformation |
|
Return the rotation component as a SciPy |
|
Compose a transformation matrix. |
Return a deep copy of the transform. |
|
|
Decompose the current transformation into its components. |
|
Compose a reflection about the x-axis. |
|
Compose a reflection about the y-axis. |
|
Compose a reflection about the z-axis. |
Set the transformation to the identity transformation. |
|
Invert the current transformation. |
|
Set the multiplication mode to post-multiply. |
|
Set the multiplication mode to pre-multiply. |
|
|
Compose a reflection matrix. |
|
Compose a rotation matrix. |
|
Compose a rotation about a vector. |
|
Compose a rotation about the x-axis. |
|
Compose a rotation about the y-axis. |
|
Compose a rotation about the z-axis. |
|
Compose a scale matrix. |
|
Compose a translation matrix. |
Attributes#
Check that the |
|
Return |
|
Return |
|
Return |
|
Return |
|
Return |
|
Return the inverse of the current transformation |
|
Return a list of all inverse transformations applied by this |
|
Get the inverse flag of the transformation. |
|
Return or set the current transformation matrix. |
|
Return a list of all current transformation matrices. |
|
Set or get the multiplication mode. |
|
Return the current number of composed transformations. |
|
Point to use when composing some transformations such as scale, rotation, etc. |
|
Return the reflection component of the current transformation |
|
Return the rotation component of the current transformation |
|
Return the rotation component of the current transformation |
|
Return the scaling component of the current transformation |
|
Return the shear component of the current transformation |
|
Return the translation component of the current transformation |